Introduction

Concept and Concept API

Conceptual Relation and Conceptual Relation API

Conceptual Graph (CG) : An introduction

CG Notations 

Integration of Standard CGIF notation in Amine

Amine MDI, multi-lingua, and multi-notations CG Editors

CG API

CG vs Predicate

Appendice 1: CG LF Grammar

Appendice 2: CG CGIF Grammar

Appendice 3: Grammar of Standard CGIF notation in Amine 

Previous: We suggest to consider first Structures and Operations (the Algebraic Layer of Amine Platform).

Introduction

This document presents three Amine structures: Concept, Relation, and Conceptual Graph (CG). Concepts and relations compose a CG, but they may be used also as a "stand-alone" structures. CG structure, notations, and basic operations are presented here, but CG matching-based operations are described in detail in CGOperations. Some details on the implementation of CG and CG operations are provided in Implementation Issues.

Thus, this document starts with Concept and Concept API, then Relation and Relation API and then CG and CG API.

Concept and Concept API

Definition: A concept is an Amine structure that implements AmineObject and Matching interfaces. It is composed of a type, an optional designator, an optional coreferent, an optional descriptor, an optional state (used in the context of Synergy language) and an optional point (the lefttop point of the rectangle that encloses the concept. It is used in the case of graphic display of the concept). In the context of a Conceptual Graph (CG), a Concept can be related to other concepts by income and/or outcome relations. Only concept type is mandatory, the other components/fields of a concept are optionals.

In analogy with classical programming, a concept corresponds to a "declaration statement" of a variable. For instance the concept [Integer :x =24] (or [Integer x 24]) corresponds to the declaration statement: Integer x =24; concept type corresponds to the declaration of variable type, concept designator corresponds to variable identifier, and concept descriptor to the value of the variable.

Concept components/fields in Amine:

• concept type is either a variable or a reference to a Type CS contained in the current ontology.

• concept designator is either null (i.e. the designator is not specified), a variable (with, by default, an existential quantifier), a reference to an Individual CS contained in the current ontology, a set of Individuals, or a pseudo-designator. Note that pseudo-designator is deprecated since Amine 6.0

• Concept coreferent (if specified) is represented by a variable shared by concepts that belong to different contexts. For instance, the two concepts [Human: khalid *x]  and    [Man ?x] can be two concepts in co-references, with x the variable that specifies this coreference. In the context of Linear and CGIF notations, Coreferents are also used in the same CG to denote several occurrences of the same concept. See CG notations and Standard CGIF notation for more detail.

• Concept descriptor is either null (i.e. it is not specified), a variable, a reference to a CS, any Amine Object (including CG) or even any Java Object.

• Concept state represents the current state of the concept, according to its concept lifecycle. This attribute is relevant only in the context of Synergy where active CGs (and concepts) are treated.

• Concept point represents the top-left point of the rectangle that will enclose the concept (if it is drawn).

• If a concept is used to compose Conceptual Graph (CG) structure, the concept can be related to other concepts by income and/or outcome relations. Note however that a concept can be used "alone", like any other Amine structure.

Definition: A context is a concept C whose descriptor is a CG g. The graph g is said to be immediately nested in C. Of course, any concept in g can be itself a context and so on, producing nested contexts at any depth.

Definition of concept in the standard definition of CG

The definition of concept in the standard definition of CG can be summarized as follows: a concept has a type and a referent. Concept type is a type label specified as primitive or defined in a type hierarchy.

The referent of a concept is specified by a quantifier, a designator, and a descriptor.

A quantifier is one of two kinds: existential or defined (which includes the universal quantifier and collections such as {Mary, John}).

A designator is one of three kinds: a) literal, which may be a number, a string, or an encoded literal; b) locator, which may be an individual marker, an indexical, or a name; c) undetermined.

A descriptor is a conceptual graph, possibly blank, which is said to describe the referent.

John Sowa provides this comment for his definition of a concept (provided above): "An existential quantifier declares that at least one instance of the type exists; a defined quantifier may specify other quantities or amounts. A designator specifies the referent by showing its form (literal) or by pointing to it (locator); an undefined designator says nothing about the referent. The three kinds of locators differ in the way the referent is determined: an individual marker, specifies a unique concept in the catalog of individuals of a knowledge base; an indexical is a symbol that determines the referent by an implementation-defined search that is not defined by this CG Standard; and a name is a symbol that determines the referent by some conventions that are independent of the current knowledge base.".

Remark: The definition of Concept in Amine is very similar to the standard definition, but some differences exist. For instance, concept type in Amine can not be a lambda expression and explicit referent quantifier is not considered (except that existential quantifier is considered by default in Amine). There are also features in Amine that are not considered in the standard definition: a concept type can be a variable and concept descriptor can be any Amine object (not only CG).

Representation, Notation and Syntax of a Concept (see CG Notations for more detail):

In versions of Amine prior to Amine 6.0, we adopted a notation for concept (and CG) that is different (in some aspects) from standard notation. For instance, in the standard notation, the designator and the descriptor are "put together" in the referent field while they are kept separate in Amine notation; one field for designator and another for descriptor. Also, the marker ":" is optional in standard notation, while it is mandatory in Amine notation. Also, a Coreferent, in standard notation, can be placed before or after a designator/descriptor. In Amine notation, it has a fixed place.

For instance, here is some examples in Amine proper notation and in Standard notation respectively:

            Amine proper notation                                    Standard notation

[Man]	[Man]
[Man :Mark]	[Man :Mark] or [Man Mark]
[Integer :sum =25]	[Integer :sum 25] or [Integer sum 25]
[Proposition = [Man]<-agnt-[Work]]	[Proposition: [Man]<-agnt-[Work]]

 

However, since Amine 6.0, standard notation is integrated in Amine. See CG notations and Standard notation in Amine for more detail.

Remark: We use brackets '[' and ']' as delimiters for both AmineList and Concept structures. In general, distinction between a list and a concept is made by syntactic analysis and by considering the context. But there is a case where the distinction is not possible: an open bracket followed by an identifier followed by a closed bracket; [Identifier] (like [Man]). Of course, if the above construct is used as a concept in a CG, it is interpreted as a concept (like [Man] in [Man]<-agnt-[Eat]; [Man] is interpreted as a concept). But if this construct occurs as an argument of a term (like pred(34, [Man], quality)) or as an element of a list, it can be interpreted as a list of one element where the element is the Identifier, or it can be interpreted as a concept where only the type is specified.  How to interpret [Man] in this case ? as a list or as a concept ? Our decision is to interpret, by default, such a construct (like [Man]) as a list. The user should precise his/her description if he/she intend another interpretation. For instance, to precise that [Man] should be interpreted as a concept (and not as a list), user can specify [Man :x] or [Man #0].

Concept API

Concept API provides two variants for most of its methods: one variant ignores variable binding and the other considers variable binding. 

Let us consider first the operations that are proper to Concept:

- constructor: several constructors are provided,

- checkers: canBeType() checks if the specified object can be a concept type, canBeDesignator() and canBeState() have the same function for concept designator and state respectively, isConcept() checks if the specified object is a Concept, isConform() checks if the specified designator is conform to the concept type, isConnected() checks if the current concept is connected to other concepts, isContext() checks if the concept is a context (its descriptor is a CG), isDesignatorSuper() checks if the designator is the keyword "super", isDesignatorThis() checks if the designator is the keyword "this", isIncomeRelation() checks if the specified relation is an income relation for the current concept, isOutcomeRelation() checks if the specified relation is an outcome relation for the current concept, etc.

- getters: getType(), getDesignator(), getDescriptor(), ..., getCoreferent() to get the coreferent (if it has one), getNbrIncomeRels() and getNbrOutcomeRels() get the number of income and outcome relations of the current concept respectively, getNbrRelations() get the sum of the number of income and outcome relations of the current concept, etc.

- setters: setType(), setDesignator(), setDescriptor(), ..., setCoreferent(), etc.

- adders: addIncomeRelation() to add the specified relation as an income relation for the current concept, addOutcomeRelation() do the same thing but for outcome relation,

- removers: removeIncomeRelation() to remove the specified relation from the income relations of the current concept, removeIncomeRelations() will do the same action for all the income relations of the current concept, removeOutcomeRelation() and removeOutcomeRelations() concern outcome relation(s) of the current concept.

- parse(): parse() parses the specified string to return the internal representation of the corresponding Concept.

- toString, toLF, and toCGIF: toString() returns by default the LF notation of the concept, toLF() returns the Linear Form (LF) notation of the concept, toCGIF() returns the CGIF notation of the concept. Recall that a concept can be a context: its description can be a CG that can be formulated in LF or in CGIF. That is why the distinction between toLF() and toCGIF() is required.

Note that parse(), toString(), toLF(), and toCGIF() methods are defined with Lexicon as parameter, to consider the multi-lingua feature of the ontology which constitutes the ontological support for any Concept.

- Implementation of AmineObject interface:

- clear() clears the concept,

- clone() performs a deep copy of the current concept,

- copy() performs a deep copy of the current concept taking into account the (optional) presence of variables (and variable binding) inside the concept.

- Implementation of Matching interface:

- Methods equals(), subsume(), unify(), maximalJoin(), and generalize() follow the same pattern and are defined in term of the generic method match(): the operation is applied recursively on the attributes of the current concept and the specified concept (i.e., match concept types, then concept designators and concept descriptors).

Also, these methods consider the (optional) presence of variables (and variable binding).

Of course, the specific definition of the operation on each concept attribute depends on the nature of the attribute (concept type can be a variable or a CS reference, concept designator can be null, a variable, an Individual reference or a DesignatorSet, concept descriptor can be null, a variable or any Amine Object).

Implementation detail on concept matching-based operations (match, generalize, maximalJoin, subsume, unify, equal) is provided in Implementation Issues.

Remark: When the value to return is an ArrayList (like children of a node in Ontology, income relations of a concept, etc.), we return an Enumeration on the ArrayList, not the ArrayList itself. Security is the main reason for this decision: if the ArrayList itself is returned, user can modify the ArrayList (change, add, remove). However, he should be able to read-only. Even Iterator over the ArrayList is not safe enough since user can remove elements from the ArrayList. With Enumeration over the ArrayList, user can read-only.

Examples

Here is excerpts from the Java class ConceptTest that calls/uses most of the methods of Concept. See BindingContext for examples on concept unification.

parse() and toString()

The Java code below provides various examples of Concept and illustrates the use of methods parse() and toString() to allow an easy and "natural" manipulation of concepts. Note that the method parse() is static and its second argument stands for the Lexicon to use in parsing. Also, the method toString() takes Lexicon as argument because the textual formulation depends on the language/lexicon to use.

The result of the code above is:

A simple concept with type only : [Man]
A simple concept with type and specific individual : [Man :karim]
A simple concept with type and a set of designators :

                                    [Man :{michael, imad, karim}]
A simple concept with type and a pseudo-designator : [Man #23]
A simple concept with type and a variable designator : [Man :x]

Parse/toString a context: recall that a context is a concept that has a CG as descriptor.

The above code returns:

A concept that is a context :

[Proposition = [Drink] -
                    -obj->[Water],
                    -agnt->[Man]
               ]

Concept and Matching operations: equal(), maximalJoin(), generalize(), etc.

Code above returns:

Concept conc1 : [Man :imad ?c = agnt(Drink, Man(imad))]
Concept conc2 : [Man :x ?d = agnt(y, Man(imad))]

Test of conc2.equal(conc1) : false

Test conc1.maximalJoin(conc2) : [Man :imad ?d = agnt(Drink, Man(imad))]

Test conc1.generalize(conc2) : [Man ?d = agnt(_v1, Man(imad))]

Test conc1.subsume(conc2) : false

Test generalizeResult.subsume(conc2) : true

Test generalizeResult.match(SUBSUME_WITH_RSLT, conc2) :

                                            [Man ?d = agnt(y, Man(imad))]

See the Java class ConceptTest for a more complete view of the call/use of most of the methods of Concept, see APIs Specification for the detailed specification of the Concept API and Implementation Issues for detail on the implementation.

Conceptual Relation and Conceptual Relation API

Definition: A conceptual relation is an Amine structure that implements AmineObject and Matching interfaces. A relation relates a concept to another concept. It is composed of a type, a source (concept), a target (concept) and a collection of points (if relation drawing is considered. Collection of points since several segments can compose the drawing of a relation) and the position of the type identifier (if graphic display is considered). Relation type, source and target concepts are mandatory.

relation type is a RelationType CS contained in the current ontology.

Conceptual relation, like concept, is used in general to compose CG but again, like a concept, a conceptual relation can be used "alone" as an Amine Object, like any other Amine structure. It can be considered as a special case of a term/predicate.

Note: In Amine CG, relation type can be a bound variable (the value should be a RelationType or a Type). This is relevant in programming context, like Prolog+CG. For reasons specified in CG operations (and especially section CG, Functional CG and CG Matching), a relation type can be even a Type CS.

Conceptual Relation API

Conceptual Relation API provides two variants for most of its methods: one variant ignores variable binding and the other considers variable binding. Let us consider first methods that are proper to Relation:

- constructors: two constructors are provided,

- getters: getType(), getSource(), getTarget(), etc.

- setters: setType(), setSource(), setTarget(), etc.

- checkers: isRelation()  to check if an object is a relation, areRelations() check if all the elements of an ArrayList are relations,

- parse(): parse a textual formulation (in LF or in CGIF) of a relation,

- toString(): returns the textual formulation (in CGIF) of the current relation,

- remove(): remove the current relation from the incomeRelations list of its target concept and from the outcomeRelations list of its source concept.

- Implementation of AmineObject interface:

- clear(): clear the relation,

- clone(): returns a deep copy of the current relation,

- copy(): returns a deep copy of the current relation,

- Implementation of Matching interface:

- the next five methods (equal(), subsume(), unify(), maximalJoin(), generalize()) follow the same pattern and they are defined in term of the generic operation match(): the operation is applied recursively on the relation types (which are Type CS references), on the source concepts and on the target concepts of the current relation and the specified relation. For instance, the maximalJoin of the current relation and the specified relation will return a new relation with the maximalJoin of the two relation types (since relation hierarchy is not considered by Matching operations, maximalJoin here will correspond to check the identity of the two relation types), the maximalJoin of the two source concepts and the maximalJoin of the two target concepts.

Implementation details on relation matching and relation matching-based operations (generalize, maximalJoin, subsume, unify, equal) are provided in Implementation Issues.

Examples:

Here is excerpts from the Java class RelationTest that calls/uses most of the methods of Relation. See BindingContext for examples on relation unification.

parse() and toString()

The Java code below illustrates the use of methods parse() and toString() to allow an easy and "natural" manipulation of relations.

The result of the code above is:

Relation rel1 : (agnt [Man] [Drink])
The same relation in French : (agnt [Homme] [Boire])

Note: the relation identifier "agnt" is an English identifier that has no synonym in French (according to our definition!). This situation could generate an error, but since we specify, by the method setMixedLanguage(true), that we allow for mixed language, the textual formulation in French will use English identifiers if necessary (since EnglishLexicon is the mainLexicon for the current ontology). This is the case for the relation with English identifier name "agnt".

Canonicity and parse() method

If the canonicity parameter is active, the method parse() checks if the utterance to parse is canonic, i.e. is conform to the canons of all concept types and relation types used in the utterance. This point is treated in more detail in CG operations. Here we illustrate it with an example :

   Relation rel1B = Relation.parse("(obj [Man] [Drink])", mainLexicon);

If the canonicity parameter is true, the parsing of the above relation will abort (and will rise an exception) because the above utterance is a violation to the canon of the concept type Drink and to the canon of the relation type obj.

Relation and Matching operations: equal(), maximalJoin(), generalize(), etc.

Code above returns:

Relation rel1 : (agnt [Man] [Drink])

Relation rel2 : (agnt [Human :imad] [Action])
Relation rel3 : (agnt [Human :imad] [Action :x])

Test of rel2.equal(rel3) : true

Test rel1.maximalJoin(rel2) : (agnt [Man :imad] [Drink])

Test rel1.generalize(rel2) : (agnt [Human] [Action])

Test rel1.subsume(rel2) : false
Test generalizeResult.subsume(rel2) : true

Test generalizeResult.match(SUBSUME_WITH_RSLT, rel2) :

                                        (agnt [Human :imad] [Action])
 

See the Java class RelationTest for a more complete example of the call/use of most of the methods of Relation, see APIs Specification for the detailed specification of the Relation API and Implementation Issues for detail on the implementation.

Conceptual Graph (CG) : An introduction

In his first book, "Conceptual Structures : Information Processing in Mind and Machines, 1984", John Sowa proposed Conceptual Graph (CG) Theory as a foundation for "high cognition". CG theory is a synthesis from several fields: semantic networks and related topics in AI, logic (Sowa showed the equivalence of CG with first-order logic and he used Existential Graph Logic of S. C. Peirce as a logical foundation for CG theory), linguistic (like various semantic networks versions, CG can be used to represent meaning and background knowledge), relational database semantic, cognitive psychology and philosophy (John showed how CG theory can represent various conceptual structures that were proposed and developed in cognitive psychology and philosophy). An updated version of CG theory, with more emphasis on ontology, philosophy and logic, is presented in John Sowa second book.

CG formalism has been used in many domains (i.e., data base semantics, natural language processing, knowledge based systems, information systems, multi-agent systems, etc.) by many groups and researchers from different countries around the world. Annual International Conferences on Conceptual Structures (ICCS) are organized since 1993.

For more detail on CG theory, see the web site of John Sowa and the online course provided by Henrik Scharfe and Peter Ohrstrom from Aalborg University, Denmark.

CG in Amine

Definition: a Conceptual Graph (CG) is an Amine structure that implements AmineObject and Matching interfaces. CG is a directed graph of nodes that correspond to concepts and labeled, oriented arcs that correspond to dyadic conceptual relations.

Differences between standard CG and Amine CG

Some differences between the standard definition of CG and Amine CG are listed below:

1. In Amine, only dyadic relations are considered. Dyadic conceptual relation has one income concept and one outcome relation. This constraint has been adopted since most of the relations are dyadic, the implementation is more simple, and monadic and more than dyadic relations can be expressed in term of dyadic relations (Figure 1). Example:

Figure 1: Tryadic relation reformulated in terms of concept and dyadic relations

2. Of course, the constraint to use dyadic relations only can be eliminated if necessary.

3. Due to the above constraint on relation, our definition of CG is a simplified version of the standard definition of CG where a CG is defined as a bipartite graph composed of two kinds of nodes: concepts and conceptual relations. In Amine, a relation is not represented by a node but by a labeled link that relates two concepts.

4. Various possibilities, concerning some extensions to the basic definition, were proposed by Sowa and also by different researchers: lambda expression as concept type, specification of various kinds of quantifiers, specification of relation cardinality, specification of uncertainty or fuzziness, etc. These elements are not considered in our definition of CG, but they can be added as needed.

5. In Amine, a variable can hold the place of a CG, of a concept type, of a concept designator, of a concept descriptor, or of a relation type. This use of variables in CG is very relevant, especially when CGs are used as first-citizen structures in a programming context like Prolog+CG and Synergy; two programming languages provided by Amine platform.

6. While Amine allow the formulation of "general" CG, it is strongly recommanded to formulate CG as functional CG, especially when CGs are used in an application that uses matching-based CG operations. Let us define first the notion of functional CG: functional CG is a CG in which income relations types of each concept are/should-be mutually different, and the same constraint should hold for outcome relations types of each concept. Consider for instance this simple example that illustrates the difference between general CG and functional CG:

       General CG:                                                    Functional CG:

     [Person]-                                 [Person]-

          -attr->[Color],                            -colorOf->[Color],

          -attr->[Weight],                           -weightOf->[Weight],

          -attr->[Sex]                               -sexOf->[Sex]

Matching based CG operations in Amine are defined on functional CG but the other operations of CG's API are defined on general CG (being functional or not). We urge the reader to see CGOperations for a detailed discussion of this important point.

6. Descriptions in Amine (CG for instance) should respect the unicity principle: only one concept should represent a specific individual in the description (in a CG). We can not have for instance in one CG two different concepts with the same individual designator. For instance, this CG is not allowed:

[Go]-

    -agnt->[Man: John],

    -instr->[Car]-poss->[Person: John]

To complete the definition of the structural part of CG structure, please note that CG in Amine has three boolean 'static attributes' (i.e. attributes that are common to all CGs):

- The static boolean attribute FunctionalCG that specifies if CGs are/should be functional (i.e. if Amine should check if CG is functional) or not. This attribute is considered in more detail in CGOperations.

- The static boolean attribute headedCG that specifies if CGs are/should be interpreted as headed CGs or not. A headed CG is a CG that contains a concept which plays the special role of the head of the CG. In Amine, the head of a headed CG will be the first concept encountered (in the textual formulation). This attribute is considered in more detail in CGOperations.

- The static boolean attribute canonicity that specifies if CGs should be canonic (i.e. if Amine should check its canonicity) or not. We consider this attribute in more detail in section CG API below.

A detailed discussion on Amine CG implementation is provided in Implementation Issues.

CG Notations

Different notations have been proposed to formulate CG. The most used ones are: Linear Form (LF), CG Interchange Format (CGIF), and Diagram Form (DF). As noted by J. Sowa, “the LF for CG is intended as a more compact notation than DF, but with good human readability”. CGIF is a simple notation for CG, intended for transmitting CGs between applications that use different internal representations.

Amine platform supports the three CG notations. At the front side, users can represent their CG in any one of them, Amine parses it and produces an internal representation (a Java object) for the CG. At the end side, Amine can formulate an internal representation of a CG in LF, CGIF, or DF. As a consequence of this flexibility in CG notation, users can provide, for instance, a CG in LF and ask Amine to return the same CG in CGIF or in DF.

Prior to Amine 6.0, we adopted a linear form that is somewhat different from LF notation proposed by John Sowa. Also, we adopted a CGIF notation that is somewhat different from Standard CGIF notation. However, the integration of standard CGIF notation to Amine has been done with Amine 6.0. In this section, we present the initial notations for LF and CGIF forms, prior to Amine 6.0. In the next section, we describe the integration of standard CGIF notation in Amine (with Amine 6.0). Please note that now (with Amine 6.0) both notations (Amine CGIF proper notation and standard CGIF notation) are allowed in Amine.

Amine LF Notation

The following example illustrates some minor differences between Sowa LF notation and Amine LF:

    According to Sowa                                                    According to Amine version

[Go]-                                          [Go]-

  (Agnt)->[Person: John]                            -Agnt->[Person: John],

  (Dest)->[City: Boston]                            -Dest->[City: Boston],

  (Inst)->[Bus]                                     -Inst->[Bus]

Instead of presenting an outcome relation like that: ->(Rel)-> , we use: -Rel->

The same holds for income relation: instead of <-(Rel)<- , we use: <-Rel-

Also, a comma ',' is used in Amine LF to separate between relations linked to the same concept. These minor differences follow the choice, taken in Amine, to consider only dyadic conceptual relation.

This section presents the main rules of Amine LF notation grammar. The complete formulation of this grammar is provided in Appendice 1.

Note: the syntactic rules presented below are presented according to the EBNF notation : (X | Y) means category X OR category Y, (X)* means 0 or several occurrences of X, {X}* means 1 or several occurrences of X, [X] means that X is optional.

CG.  A CG is a concept with zero, one or several related relations. A relation points to a concept that can be related itself to other relations and so on.

RLF1. CG =  Concept  [Relation | Relations] .

Concept. A concept is delimited by square brackets '[' and ']'. The first element is the concept type, followed possibly by the concept designator prefixed by colon ':',  followed possibly by a pseudo-designator prefixed by '#', followed possibly by a co-reference, and followed possibly by concept descriptor prefixed by equal '='.

RLF2. Concept ::= "[" Type  [":" Designator]   ["#" PseudoDesignator]   [CoReferent]    ["=" Descriptor]  "]" .

A designator is either an individual identifier, a set of individual identifiers, or a variable identifier. A Pseudo-designator is a sequence of characters. A coreferent is a variable prefixed by '*' or '?'. A descriptor is any Amine Object (including CG) or a variable.

RLF3. Designator ::=  IndividualIdent | SetOfIndividualIdent | Variable .

RLF4. CoReferent ::=  ("*" | "?") Variable .

RLF5. Descriptor ::=  Amine_Object | Variable .

Examples of concepts:

Concept with type only: [Man]

Concept with type and individual identifier: [Man : John]

Concept with type and set of individuals: [Man : {John, Carl, Henry}]

Concept with type and variable designator:  [Cat : x]

Concept with type and pseudo-designator:  [Cat  #3]

Concept with type and coreferent: [Cat  *c]

Concept with type, individual identifier and a coreferent:  [Man : John *c]

Two examples of concepts with type, individual identifier and descriptor:

[Date :CurrentDate = [04,01,2000]]

[Proposition :propHenry 

      = [Man : Carl]<-agnt-[Think]-obj->[Proposition = 

                                            [Man: Carl]-attr->[Crazy] ] ]

Concepts with type and descriptor:

[Integer = 25]

[List = [1, 2, 3]]

[Term = papa(x, Hicham)]

Pseudo-designator: sometimes and due to the textualization of a CG (in LF or CGIF), the same concept occurs many times in the description. Concepts with the same designator (i.e. the same individual identifier, the same set of individuals or the same variable) are occurrences of the same concept. But two 'generic' concepts with the same concept type and without designator (like [Person] and [Person]) are not necessary occurrences of the same concept: a default existential interpretation is applied to them; the two concept can refeer to entities that are not necessary the same.

One solution to specify that two (or more) 'generic' concepts are occurrences of the same concept is to use the same variable as designator for all concept occurrences. Note that such a variable is usefull only in LF (and CGIF) for the identification of occurrences of the same concept, it will not occur in the diagram form of the same CG, neither in the internal representation of the CG. The drawback of this solution is an extensive use of extra variables (space is allowed to each variable and extra-treatment is done accordingly). To avoid this extra-space and treatment, Amine offers another solution: the use of a “marker” (called pseudo-designator) that play this secondary role. Pseudo-designator is used in the LF and CGIF forms only, it is not represented in the internal representation. Here is an example of a CG with the pseudo-designator “#1”.

[Extract]-
    -agnt->[Person],
    -obj->[Inanimate  #1]-matr->[Wood],
    -manr->[Strong],
    -target->[Inanimate]-on->[Inanimate  #1]-priceOf->[Expensive]

Note: Pseudo-designator is specific to "Amine concept/CG notation", it is not allowed in the standard notation. In standard notation, user should use coreferents (instead of pseudo-designators). See Standard notation in Amine for more detail.

Conceptual relation. A conceptual relation of type R, with source concept C1 and target concept C2 is expressed as follows: [C1]-R->[C2] or [C2]<-R-[C1]. The relation type R and the source concept are separated by a hyphen “-” while an arrow separates R from the target concept (the arrow is directed toward the target concept).

RLF6. Relation ::= ("-" RelationType  "->" CG) |  ("<-" RelationType  "-" CG) .

RLF7. RelationType  ::= RelTypeIdentifier | TypeIdentifier | Variable .

Example: the agent of Walk is Girl Fouzia:  [Girl : Fouzia]<-agent-[Walk]    

A concept can be connected to several relations. If a concept C is connected to several relations, it is linearized as follows: C should be followed by a hyphen "-" and then the formulation of its relations (as if each relation is directly related to C). The relations are separated by comma “,” and the last relation should end, if other relations that are not connected (directly) with C follow, with a semicolon “;” (instead of comma ","). Thus, the hyphen "-" and the semicolon “;” play the role of delimiters to enclose all relations related to a concept.

RLF8.  Relations ::=  "-"  Relation  {"," Relation}*  [";"] .

Example:

[Work]-

    -agnt->[Person: Jane]-

                                -ageOf->[Age = 30],

                                <-poss-[House : myHouse];

    -near->[House : myHouse]

Remarks:

1. The target concept of a relation (for instance, [Person: Jane] in the example above) can be related to other relations and so on. The whole CG is formulated in this way.

2. As illustrated by the above example, semicolon “;” is used to specify the end of relations that should be related to the current “open” concept ([Person: Jane] for instance). A semicolon specifies that we have to move-up to the antecedent level. Moreover, semicolon ";" play also the role of comma ",". This is the case for instance for the relation: -agnt->[Person:Jane]...; in the example above.

3. Tabulation and carriage-return are used only for "pretty-print"; they are not considered in the analysis of the notation.

Amine CGIF notation

In previous versions of Amine (before Amine 6.0), only a subset of the CGIF standard was considered. We comment in this section the main syntaxic rules of this subset. See standard CGIF definition for the required background. The complete formulation of the grammar is provided in Appendice 2. In the next section we describe the integration of Standard CGIF notation in Amine (starting with Amine 6.0).

CG. CG is expressed in CGIF as a list of concepts and of relations. The elements in this list can be in any order provided that defining nodes/concepts precede the bounded nodes/concepts.

RCGIF1. CG ::= {Concept | Relation}*  .

Concept. A concept in CGIF is expressed in the same way as in LF notation.

Conceptual relation. A conceptual relation begins with a left parenthesis "(" followed by the relation type and two arguments. It ends with a right parenthesis ")".

RCGIF2. Relation  ::=  "(" RelationType  Argument  Argument  ")" .

An argument of a relation is a concept, a concept designator (the related concept in this case should be specified before the relation), or a pseudo-designator.

RCGIF3. Argument ::=  Concept | Designator | Pseudo-designator .

Examples of CGIF :

  [Go   #0]

  (Agnt  #0  [Person: John]) (Dest #0   [City: Boston]) (Inst  #0   [Bus])

Notet the use of pseudo-designator to allow several occurrences of a concept. Of course, a variable can be used also, but it would be an unnecessary consommation of ressources.

Another example: CGIF form for a CG that was described previously :

[Work #1] [Person: Jane] [House : myHouse]

(agnt #1 Jane)  (near  #1  myHouse)  (ageOf  Jane  [Age = 30]) 

(poss  myHouse  Jane)

As illustrated by the above example, a concept with an individual identifier as designator can be refeered by this identifier without using in addition a pseudo-designator. The same holds if the designator is a variable. There is however some exception: in some special case, like the use of the parameter "super" to designate genus in a definition (especially when the definition contains several genus), different concepts can have "super" as designator. In this case, the use of a pseudo-designator beside the parameter is necessary. Consider for instance this example:

[System :super#0] [Intelligent :super#1] [Build #2]
(obj #2 super#0) (agnt #2 [AIScientist]) (attr super#0 super#1)

Amine CG Display Form notation

See CG Drawing editor for more detail.

Integration of Standard CGIF notation in Amine

Integration of Standard CGIF notation in Amine (since Amine 6.0) involves many other integrations/additions (like a mapping for actors and a mapping for n-adic relations with n > 2). We discuss them in this section.

From Amine CGIF to Standard CGIF notation

Instead of pseudo-designator, standard CGIF notation makes use of coreferent. For instance, instead of the pseudo-designator #1 in this example:

[Work #1] [Person: Jane] [House : myHouse]

(agnt #1 Jane)  (near  #1  myHouse)  (ageOf  Jane  [Age = 30])  (poss  myHouse  Jane)

Standard CGIF notation will use a coreferent:

[Work *p] [Person: Jane] [House : myHouse]

(agnt ?p Jane)  (near  ?p  myHouse)  (ageOf  Jane  [Age:30]) (poss  myHouse  Jane)

Coreferent in Standard CGIF has two functions:

• It is used in CGIF notation (and LF notation) to specify occurrences of the same concept in the same CG. Such a coreferent does not exist in the Display form, nor in the internal representation of the CG. It has the function of the pseudo-designator, introduced above.

• It is used to specify coreference link between concepts that belong to embeeded CGs.

Also, in standard CGIF notation, coreferent, designator and descriptor share the same and one field; the field after the concept type. In standard CGIF notation, no separator is used to introduce and differentiate between the designator and the descriptor. Also, the separator ":" is optional and there is a great flexibility in ordering coreferent, designator and descriptor; a coreferent can be placed before or after the designator and/or the descriptor.

To assure compatibility with versions anterior to Amine 6.0 (that use proper Amine CGIF notation), Amine 6.0 adopts a CGIF syntax that integrates standard CGIF notation and "Amine proper CGIF notation". A CG that was stored in "Amine proper CGIF notation" is still readable by Amine, but it will be "recycled" in standard CGIF notation (i.e. a new save of the CG, in CGIF, will use standard CGIF notation).

Here is the syntaxic grammar of a concept in Standard CGIF notation in Amine:

Comment: A concept can start with a comment and terminates with an end comment. A coreferent can be stated before or after the separator ":", before or after a designator, and before or after a descriptor. Separators ":" and "=" are optionals. Parameter modes (proper to Synergy), States (proper to Synergy), and Point (proper to diagram form) can be specified inside the concept or in the end comment.

Note that the above syntaxic rule is used to define the syntax of concepts in both CGIF and LF notations. Thus, with Amine 6.0 we adopt the above syntaxic rule for the representation of concept in both LF and CGIF forms.

Examples:

Example #1

The classical example of John Sowa ("John Go to Boston by Bus") is presented according to the Diagram Form notation (Figure 2), the LF notation and the Standard CGIF notation.

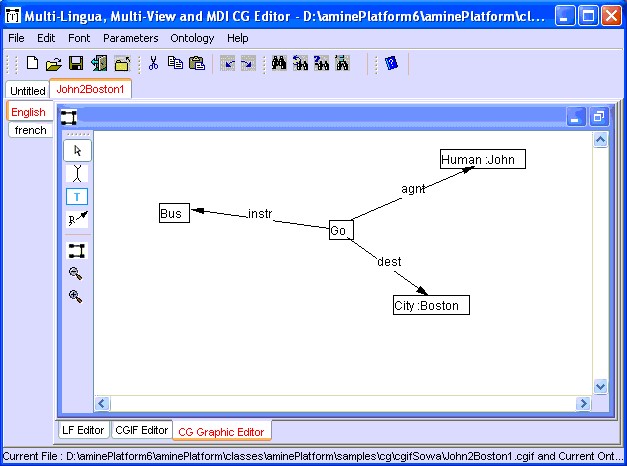
Figure 2: Diagram Form of a CG (in Amine)

LF notation:

[Go] -
    -instr->[Bus],
    -dest->[City :Boston ],
    -agnt->[Human :John ]

Standard CGIF notation (without graphical information):

[Go : *p1 ]
(instr ?p1 [Bus]) (agnt ?p1 [Human :John ]) (dest ?p1 [City :Boston ])

Standard CGIF notation (with graphical information):

[Go : *p1 ; & 235 89]
(instr ?p1 [Bus ; & 65 72]; (154 87)(235 97)(97 78)) (dest ?p1 [City :Boston ; & 299 164]; (283 135)(253 106)(334 164)) (agnt ?p1 [Human :John ; & 346 18]; (307 62)(255 89)(380 35))

Note that graphical information, for both concepts and relations, are specified in the EndComment.

Example #2

Here is another example proposed by John Sowa to illustrate nested CG:

LF notation:

[Believe] -
    -expr->[Human : "Tom" ],
    -thme->[Proposition : [Want] -
                                -expr->[Human : *x3 "Mary" ],
                                -thme->[Situation : [Marry] -
                                                        -agnt->[Woman : ?x3 ],
                                                        -thme->[Sailor]
                                        ]
            ]

Standard CGIF notation:

[Believe : *p1 ]
(expr ?p1 [Human : "Tom" ]) (thme ?p1 [Proposition : [Want : *p2 ]
                                         (expr ?p2 [Human : *x3 "Mary" ])

                                         (thme ?p2 [Situation : [Marry : *p3 ]
                                                        (agnt ?p3 [Woman : ?x3 ]) (thme ?p3 [Sailor])

                                                   ])
                                       ])

Let us consider again the definition of type "Intelligent_System" which has two genus, and how coreferent can be used instead of pseudo-designator:

In LF:

    [System : *p1 super ] -
                    -intelligenceOf->[Intelligent : *p2 super ],
                    <-obj-[Build]-agnt->[AIScientist]

In Standard CGIF notation:

    [System : *p1 super ] [Build : *p3 ]
    (obj ?p3 ?p1 ) (agnt ?p3 [AIScientist]) (intelligenceOf ?p1 [Intelligent : *p2 super ])

With the integration of Standard CGIF notation in Amine, we enhance the interoperability between Amine and other CG tools that adopt also Standard CGIF notation.

Appendice 3 provides the grammar for Standard CGIF notation in Amine. See also Synergy for a brief discussion about the interoperability between Amine and CharGer. This interoperability is accomplished thanks to the adoption of Standard CGIF notation by the two tools.

Standard CGIF notation, Actors and "active concepts"

Actors constitute a standard element in CG theory, like concepts and relations. Standard CGIF notation provides a precise syntax for their representation. In Amine, we adopt another perspective: a concept can represents a static or a dynamic/activable entity (operation, function, process, etc.). Thus, we use concepts to represent both "static concepts"  and actors (dynamic/activable concepts). See Synergy for more detail.

Now that Amine integrates Standard CGIF notation (with Amine 6.0), we provide a mapping between "CG with actors" and "Amine CG (with activable concepts)": "CG with actors" formulated in Standard CGIF notation is translated to "Amine CG". Figure 3 provides an example that illustrates this mapping: Figure 3.a shows CharGer diagram notation of a CG with actors

(a) CharGer diagram notation of a CG with actors    

( /* <actor id="35979485996" owner="35979485989"> <type> <label>minus</label> </type> <layout> <rectangle x="185.0" y="150.0" width="60.0" height="25.0"/> <color foreground="0,0,0" background="255,255,255"/> </layout> </actor> */ minus 99 20 | 79)        

(b) CharGer formulation of the above CG in Standard CGIF notation

(c) Amine reformulation of a CG with actors in Amine, after the automatic translation of its CGIF notation

Figure 3: Reformulation in Amine of a CG with actors

Please note that an actor can have more than one output. See Synergy for more detail.

Standard CGIF notation, more than dyadic relations and their reformulation in Amine

CG theory allows for conceptual relations that are more than dyadic, like the classical example of "Between" relation. Standard CGIF notation allows for the representation of more than dyadic relations. In Amine we consider dyadic relations only.

Now that Amine 6.0 integrates Standard CGIF notation, we provide a mapping between "CG with more than dyadic relations" and "CG with dyadic relations only": "CG with more than dyadic relations" formulated in Standard CGIF notation is translated to "CG with dyadic relations only". This mapping is based on the representation of "more than dyadic relation" by a concept and dyadic relations. With this mapping, we can say now that Amine handles nadic relations (with n > 2).

Figure 4 provides the example of Between relation (with Betw as a synonym).

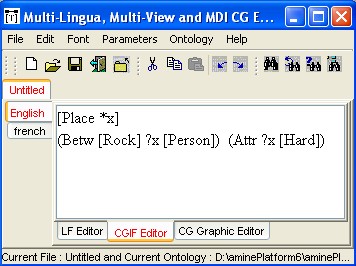
          (a) Diagram notation of a Triadic relation                                              (b) Triadic relation in Standard CGIF notation

(c) Reformulation of Triadic relation in Amine, after the automatic translation of its CGIF notation

Figure 4: Reformulation in Amine of a Triadic relation

Remark:

Integration of Standard CGIF notation to Amine is not complete; for instance "null" is not allowed as a concept type, monadic expression is not allowed as a concept type, monadic relation is not allowed (it should be expressed as a dyadic relation),  cardinality is not considered, quantifier is not considered, etc. Some of these features may be integrated in the next versions of Amine.

Interoperability between Synergy and CharGer

CharGer 3.6 provides the possibility to store CG in Standard CGIF notation but it doesn't provide possibility to read a CG from its Standard CGIF notation. Amine 6.0 provides the possibility to read a CG from and store a CG in Standard CGIF notation.

Through Standard CGIF notation, it is now possible to establish an interoperability between Amine and CharGer. Here is somple examples that illustres this new possibility. See Synergy for a complement.

Figure 5.a shows a simple CG in CharGer, according to its diagram notation. Figure 5.b shows the formulation of this CG in Standard CGIF notation, formulation produced by CharGer. The Standard CGIF notation produced by CharGer was then read by Amine. Figure 5.c shows the diagram display of the same CG by Amine (after the read of the file that contains the Standard CGIF notation of the CG, and the automatic drawing of the CG).

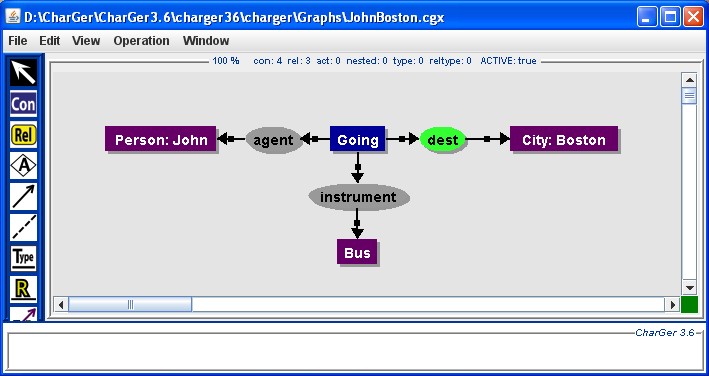
(a) Simple CG in CharGer diagram notation

(c) Automatic drawing and display of the CG by Amine CG Editors GUI

Figure 5: Mapping of a simple CG, from CharGer to Amine, through Standard CGIF notation

A second example illustrates the case of composed CG (or compound CG; embeeded CG).

(a) Compound CG in CharGer diagram notation

(b) CharGer formulation of the above CG in Standard CGIF notation

(c) Automatic drawing and display of the CG by Amine CG Editors GUI

Figure 6: Mapping of a compound CG, from CharGer to Amine, through Standard CGIF notation

Consult document Synergy for examples of mapping CG with actors to "Amine CG (with activable concepts)".

Amine MDI, multi-lingua, and multi-notations CG Editors

Amine provides an MDI, multi-lingua, and multi-notations CG editors that allow the edition of several CGs. A CG can be edited in LF, CGIF, or DF, and it can be edited also according to a specific language among the languages associated to the current ontology. Users can switch from one CG notation to another and from one language to another (i.e. they can express their CG in French and then ask Amine to translate it in English or in Danish). See Multi-lingua and multi-notations CG Editors GUI for a detailed description of this CG notations Editors GUI.

CG API

Like the other Amine structures, CG API implements AmineObject, Matching, and DescriptionWithGenus interfaces and provides two variants for most of its methods: one variant ignores variable binding and the other considers variable binding.  Let us consider first the operations that are proper to CG:

- constructor: several constructors are provided to create a CG,

- getters: getFunctionalCG() to get the value of the static attribute functionalCG, getHeadedCG() to get the value of the static attribute headedCG, getHead() to get the head of the CG if this later is a headed CG, getConcept() to get from the current CG a concept with type and designator that are equal to the specified type and designator, getConceptWithType() to get from the current CG a concept with a type that is equal to the specified type, getConceptWithDesignator() to get from the current CG a concept with a designator that is equal to the specified designator, etc. getRelations() returns all relations of the current CG, getRelationsInHmp() returns in a HashMap all relations of the current CG, relations are stored in the HashMap according to their types (the key), getNbrConcepts() returns the number of concepts contained in the current CG, getNbrRelations() return the number of relations contained in the current CG, etc.

- finders: While methods getXXX() above use the method equals() to test reference identity, methods findXXX() use the method equal() which is a matching operation, to find a concept in the current CG: findConcept() finds the (first) concept in the current CG that is equal (in content) with the specified concept, findConcepts() finds all concepts in the current CG that are equals (in content) with the specified concept, findConceptWithType() finds the (first) concept in the current CG with type equal to the specified type, findConceptsWithType() finds all concepts in the current CG with type equal to the specified type, findConceptWithDesignator() finds the (first) concept in the current CG with designator equal to the specified designator, findConceptsWithDesignator() finds all concepts in the current CG with designator equal to the specified designator, findRelations() finds all the relations in the current CG wih the specified type, etc.

- checkers: isConceptInCG() checks if the specified concept is contained in the current CG, isEmpty() checks if the CG has no concept, isAConcept() checks if the current CG contains only one concept and no relation, isARelation() checks if the current CG contains only one relation with its source and target concepts, isRelationInCG() checks if the specified relation is contained in the current CG, etc.

- adders: addConcept() adds the specified concept to the current CG, addRelation() adds the specified relation to the current CG,

- replaceConcept(): replaces a concept by another concept in the current CG,

- removers: removeConcept() removes the specified concept from the current CG, removeRelation() removes the specified relation from the current CG,

- setters: setConcepts() to set an array of concepts to the current CG, setFunctionalCG() to set a value to the functionalCG attribute, setHeadedCG() to set a value to the headedCG attribute, setCanonicity() to set a value to the canonicity attribute,

- Load/Save: load()/open() loads a CG from the specified file, store()/save() stores the current CG in a specified file,

- I/O: parse() parses the textual formulation of a CG (it can be in LF or in CGIF), parseCGIF() parses a CGIF form, parseLF() parses a LF. If the static attribute functionalCG is true, method parseXXX() checks if the CG is functional or not. If the static attribute canonicity is true, methods parseXXX() check if the parsed CG is canonic or not.

- I/O: toString(), toLF(), and toCGIF(). toCGIF() returns a CGIF textualization of the content of the current CG, toLF() returns a LF textualization of the content of the current CG, toString() calls toLF() by default.

parseXX() and toXX() methods have Lexicon as parameter, to consider the multi-lingua feature of the ontology which constitutes the ontological support for any CG.

- conversion: toConcept() and toRelation(). toConcept() returns the concept that composes the current CG (if the current CG is composed of only one concept), toRelation() returns the relation that composes the current CG (if the current CG is composed of only one relation),

- selectHead(): selects the most connected concept from the current CG,

- canonical formation rules:

- restrictType() restricts the type of the specified concept in the current CG to the specified type. The specified type should be a subtype of the concept type.

- restrictDesignator() restricts the designator of the specified concept in the current CG to the specified designator. The specified designator should be conform to the concept type.

- restrictDescriptor() restricts the descriptor of the specified concept in the current CG.

- generalizeType() generalizes the type of the specified concept in the current CG to the specified type. The specified type should be a supertype of the concept type.

- generalizeDesignator() generalizes the designator of the specified concept in the current CG.

- generalizeDescriptor() generalizes the descriptor of the specified concept in the current CG.

- analogizeType() replaces by analogy the type of the specified concept in the current CG by the specified type. The two types should have a common superType (different from the ontology root).

- join() joins two CGs around two identical concepts. Copy, add, and detach (remove) have been introduced before.

- Implementation of DescriptionWithGenus interface:

- getGenus() gets genus concept types if the current CG corresponds to the definition body of a concept type (note that a type can have several genus, not only one).

- Implementation of AmineObject interface:

- copy and clone: clone() performs a deep copy of the current CG, copy() performs a deep copy taking into account variable binding and values of variables,

- clear(): clear the content of the current CG,

- getVariables() gets the variables used in the current CG.

- Implementation of Matching interface: the definition and implementation of Matching methods; match(), equal(), subsume(), subsumeWithResult(), maximalJoin(), generalize(), and unify() are provided in CGOperations.

Other CG operations:

- specialize(): specialize a CG g1 by a maximal join with another CG g2. Contrary to maximalJoin(), specialize does not create a new CG but modifies g1 itself.

- generalise(): generalise a CG g1 by a generalization with another CG g2. Contrary to generalize(), generalise does not create a new CG but modifies g1 itself.

- expand(): two versions of expand are provided, one for concept type and another for relation type. 

- isCanonic(): The method isCanonic() checks if the current CG g is canonic, i.e. if (specified) canon of each concept type and relation type used in g subsumes g.

See NewCGOperations for new CG operations (contract(), analogy(), compare(), and coveredBy()), available since Amine 3.

Examples:

Here is excerpts from the Java class CGTest that calls/uses most of the methods of CG API. See CGOperations for examples on matching-based CG operations and BindingContext for examples on CG unification.

Note that the following examples make use of "Amine proper CGIF notation".

parseXXX() and toXXX()

- parse() and toString(): The Java code below illustrates the use of methods parse() and toString() to allow an easy and "natural" manipulation of CG. Like Concept and Relation examples, we start by loading an ontology and choosing the lexicon to use in parsing and in expressing the CG. The method parse() determines the type of the notation (LF or CGIF) and then calls the appropriate parsing method (parseLF() or parseCGIF()). The method toString() calls by default the method toLF().

   

The result of the code above is:

A simple CG cg1 : [Man :imad]<-agnt-[Drink]

The same CG cg1 but expressed in French: get the lexicon of French, set the ontology boolean parameter MixedLanguage to true (in order to use English words if no French synonym exist) and then call toString() to formulate the CG in French:

Lexicon frenchLexicon = ontology.getLexicon(Identifier.wrap("french"));
ontology.setMixedLanguage(true);
System.out.println("The same CG cg1 in French : " +
                                    cg1.toString(frenchLexicon));

The result of the code above is:

The same CG cg1 in French :

[Homme :imad]<-agnt-[Boire]

parse(), parseLF(), parseCGIF(), toString(), toLF(), and toCGIF()

As noted previously, parse() determines, from the string in input, the nature of the CG notation and then call parseLF() or parseCGIF(). Also, toString() calls toLF() by default. However, the user can call toLF() or toCGIF() to get a CG in a specific notation. Let us consider some examples of these operations.

Note that the CG in input is in LF:

CG cg1 = CG.parse("[Man:imad]<-agnt-[Drink]", mainLexicon);
System.out.println("\nFrom LF input to LF output: \n" +

                                        cg1.toString(mainLexicon));
 

Note that the CG in input is in CGIF:
cg1 = CG.parse("(agnt [Drink] [Man:imad])", mainLexicon);
System.out.println("\nFrom CGIF input to LF output: \n" +

                                        cg1.toLF(mainLexicon));

cg1 = CG.parseLF("[Man:imad]<-agnt-[Drink]", mainLexicon);
System.out.println("\nFrom LF input to CGIF output: \n" +

                                        cg1.toCGIF(mainLexicon));
 

The result of the code above:

From LF input to LF output:
[Man :imad]<-agnt-[Drink]

From CGIF input to LF output:
[Drink]-agnt->[Man :imad]

From LF input to CGIF output:
(agnt [Drink] [Man :imad])

A more complex example:
CG cg2 = CG.parse("[Drive]-\n" +
                        "-obj->[Car],\n" +
                        "-agnt->[Man: imad]-attr->[Intelligent],\n" +
                        "-manr->[Fast]", mainLexicon);
System.out.println(

    "\nFrom LF input to LF output (a more complex example): \n" +
    cg2.toLF(mainLexicon));

cg2 = CG.parseLF("[Drive]-\n" +
                        "-obj->[Car],\n" +
                        "-agnt->[Man: imad]-attr->[Intelligent],\n" +
                        "-manr->[Fast]", mainLexicon);
System.out.println(

    "\nFrom LF input to CGIF output (a more complex example): \n" +
    cg2.toCGIF(mainLexicon));

cg2 = CG.parseCGIF("[Drive #0] [Man :imad] " +
                   "(agnt #0 imad) (obj #0 [Car]) " +

                   "(manr #0 [Fast]) (attr imad [Intelligent])",

                    mainLexicon);
System.out.println(

    "\nFrom CGIF input to LF output (a more complex example): \n" +
    cg2.toLF(mainLexicon));
 

The result of the code above:

From LF input to LF output (a more complex example):
[Drive] -
    -obj->[Car],
    -agnt->[Man :imad]-attr->[Intelligent],
    -manr->[Fast]

From LF input to CGIF output (a more complex example):
[Drive #0] [Man :imad]
(attr imad [Intelligent]) (manr #0 [Fast]) (agnt #0 imad) (obj #0 [Car])

From CGIF input to LF output (a more complex example):
[Drive] -
    -agnt->[Man :imad]-attr->[Intelligent],
    -obj->[Car],
    -manr->[Fast]

parse() and the parameter functionalCG

Methods parse(), parseLF() and parseCGIF() consider the parameter functionalCG: if functionalCG is true, parseXXX() checks if the input CG is a functional CG. If functionalCG is false, no check is done. Consider the following example: the static method setFunctionalCG() sets the attribute functionalCG to false. parse() will parse the CG without checking if it is functional or not (in our example, it is not functional).

CG.setFunctionalCG(false);
cg2 = CG.parse("[Drive]-\n" +
                    "-obj->[Car],\n" +
                    "-agnt->[Woman],\n" +
                    "-agnt->[Man: imad]-attr->[Intelligent],\n" +
                    "-manr->[Fast]", mainLexicon);
System.out.println("Example of non functional CG :\n" + cg2.toString(mainLexicon));

The result of the code above:

Example of non functional CG :

[Drive] -
    -obj->[Car],
    -agnt->[Woman],
    -agnt->[Man :imad]-attr->[Intelligent],
    -manr->[Fast]

However, the parsing of the same CG but with functionalCG attribute true, by CG.setFunctionalCG(true), will provide this message:

Error: Relation agnt exists already or functional CG violation.

parse() and the parameter Canonicity

The following code illustrates the case of canonicity violation: if CG canonicity parameter is true, the method parse() checks if the CG is canonic or not. In the following example, the CG is not canonic because the object of Drink can not be Color.

CG cg1B = null;
try {
 
  System.out.println(cg1B.toString(mainLexicon));
}
catch (Exception ex) {
  System.out.println(ex.getMessage());
}

The result of the code above is:

Error: the current structure is not canonic

However, the parsing of the same CG will succeed if the canonicity attribute was set to false, by CG.setCanonicity(false).

Find Concept and Replace Concept

- Find a concept in a CG according to its type: findConceptWithType()

Assume the above CG cg1B. The next two statements enable the localization of the concept [Drink] in cg1B:
  Type drinkType = mainLexicon.getTypeCS(Identifier.wrap("Drink"));
  Concept concDrink = cg1B.findConceptWithType(drinkType);
 

- Find a concept in a CG that is equal (in content) to the specified concept: FindConcept()

Find a concept in the CG cg1B that is equal to the concept [Drink]:

  Concept concDrk = Concept.parse("[Drink]", mainLexicon);

  Concept concDrink = cg1B.findConcept(concDrk);

- replace a concept by another concept in a CG: replaceConcept()

Replace the concept [Drink] in the CG cg1B by the concept [Look]: this operation involves first the localization of the concept [Drink] in the CG cg1B and the creation of the concept [Look]:

Concept concLook = Concept.parse("[Look]", mainLexicon);
cg1B.replaceConcept(concDrink, concLook); // concept [Drink] was already localized
System.out.println("cg1B after replacing [Drink] by [Look] :\n" +    

                                            cg1B.toString(mainLexicon));

Result of the above code:
cg1B after replacing [Drink] by [Look] :
[Look] -
    -obj->[Color],
    -agnt->[Man :imad]

Copy of a CG

The result of the code above is:

copy of the simple CG cg1 :
[Man :imad]<-agnt-[Drink]

Addition of Concept/Relation

- addition of a new concept to a CG: addConcept()

 System.out.println(

    "The CG copyOfCG1 after the addition of the concept [Water]: \n" +

    copyOfCG1.toCGIF(mainLexicon));
 

The result of the above code is:

The CG copyOfCG1 after the addition of the concept [Water]:
[Water]
(agnt [Drink] [Man :imad])

- addition of a new relation to a CG: addRelation()

Add the relation [Drink]-obj->[Water] to the CG copyOfCG1: The first step is to locate the concept [Drink] in the CG copyOfCG1.
  Type drinkType = mainLexicon.getTypeCS(Identifier.wrap("Drink"));
  Concept concDrink = copyOfCG1.findConceptWithType(drinkType);

The second step is the addition of the relation, with type obj, to the CG copyOfCG1:
RelationType relObjType =         

                mainLexicon.getRelationTypeCS(Identifier.wrap("obj"));

Result of the code above:

Note: The CG copyOfCG1 after the addition of the relation [Drink]-obj->[Water] :

[Drink] -
    -agnt->[Man :imad],
    -obj->[Water]

Remark: to perform this addition, one may propose to parse the relation and then add it to the CG like that:  copyOfCG1.addRelation(Relation.parse("(obj [Drink] [Water])", mainLexicon));

The problem with this proposition is that the two concepts [Drink] and [Water] in the relation will not be the same as those in the CG copyOfCG1.

- addition of a new relation by the use of join operation: join()

Recall that the CG cg1B is:

[Look] -
    -obj->[Color],
    -agnt->[Man :imad]

Add the relation [Look]-manr->[Fast] to the CG cg1B: The first step is to locate the concept [Look] in the CG cg1B. Also, the relation is considered as a CG to join with the CG cg1B around the identical concept [Look]:

Concept concLookIn_cg1B = cg1B.findConcept(concLook);
CG cgj = CG.parse("[Look]-manr->[Fast]", mainLexicon);
Concept concLookIn_cgj = cgj.findConcept(concLook);

System.out.println("result of join:\n" +

                                cgRsltJoin.toString(mainLexicon));
 

The result of the code above:

result of join:

[Look] -
    -obj->[Color],
    -agnt->[Man :imad],
    -manr->[Fast]

Remark: The new relation is not added to the CG cg1B, it is added to a copy of the CG cg1B.

GetXXX()

- Get all concepts of a CG: getConcepts()

The method getConcepts() returns an Enumeration over all the concepts of the CG. The instruction for is used to scan the enumeration and to perform a treatment on the concepts. In this example, the treatment is a call to the method toString() to get the textual formulation of concept.

System.out.println("Get all the concepts of the CG copyOfCG1 :");
Concept conc = null;
for (Enumeration e = copyOfCG1.getConcepts(); e.hasMoreElements();) {
    conc = (Concept) e.nextElement();
    System.out.println(conc.toString(mainLexicon));
}

The result of the above code:

Get all the concepts of the CG copyOfCG1 :
[Man :imad]
[Drink]
[Water]

- Get all relations of a CG: getRelations()

The method getRelations() returns an Enumeration over all the relations of the CG. The instruction for is used to scan the enumeration and to perform a treatment on relations. In this example, the treatment is a call to the method toString() to get the textual formulation of relation.

System.out.println("Get all the relations/branches of the CG copyOfCG1 :");
Relation relation = null;
for (Enumeration e = copyOfCG1.getRelations(); e.hasMoreElements();) {
    relation = (Relation) e.nextElement();
    System.out.println(relation.toString(mainLexicon));
}

The result of the code above:

Get all the relations/branches of the CG copyOfCG1 :
(agnt [Drink] [Man :imad])
(obj [Drink] [Water])

- Select Head or the most connected concept in a CG: selectHead()

System.out.println("Select a head (a concept) for the CG copyOfCG1 : " +
                    copyOfCG1.selectHead().toString(mainLexicon));

The result of the code above:

[Drink]

Canonical Formation Rules/Operations

- restrict the type of a concept in a CG: restrictType()

The CG used in this example is:

 cg1 : [Drive]-
            -obj->[Object],
            -agnt->[Person]
 

The goal is to restrict in cg1 the type Object of the concept [Object] to the type Car. This goal is achieved in several actions:

action #1: get, from the current lexicon, the Type CS with the identifier name "Object"
Type objectType = mainLexicon.getTypeCS(Identifier.wrap("Object"));

action #2: get the concept in cg1 with type Object
Concept concToRestrict = cg1.getConceptWithType(objectType);

action #3: get, from the current lexicon, the Type CS with the identifier name "Car"
Type carType = mainLexicon.getTypeCS(Identifier.wrap("Car"));

action #4: do the restrictType operation
cg1.restrictType(concToRestrict, carType);

System.out.println("cg1 after the restriction :\n" +   

                                        cg1.toString(mainLexicon));

The result of the above code:

cg1: [Drive]-
          -obj->[Car],
          -agnt->[Human]

Note: If we attempt to restrict, for instance, the type Car of the concept [Car] in cg1 to the type Bus, restrictType() operation will not perform the restriction because Bus is not a subtype of Car.

- restrict the designator of a concept in a CG: restrictDesignator()

Assume the above CG cg1 with the goal to restrict in cg1 the designator of the concept [Human] to imad. Again, this goal is achieved in several actions:

action #1: get, from the current lexicon, the Type CS with the identifier name "Human"

 Type humanType = mainLexicon.getTypeCS(Identifier.wrap("Human"));

action #2: get the concept in cg1 with type Human
concToRestrict = cg1.getConceptWithType(humanType);

action #3: get, from the current lexicon, the Individual CS with the identifier name "imad"
Individual imadIndividual =

                    mainLexicon.getIndividualCS(Identifier.wrap("imad"));

action #4: do the restrictDesignator operation
cg1.restrictDesignator(concToRestrict, imadIndividual);

The result of the code above:

cg1: [Drive] -
        -obj->[Car],
        -agnt->[Human :imad]

Note: restrictDesignator() will fail if the designator is not conform to the concept type. For instance, if "imad" was a cat, the above restriction will fail.

- generalize the type of a concept in a CG: generalizeType()

generalizeType() is the inverse of restrictType(). Let us assume the above CG cg1 and the goal to generalize the type Car of the concept [Car] to the type Vehicle. Like the examples above, we have to get first the concept [Car] from cg1 and the the Type CS with identifier name Vehicle. Then we can call generalizeType():

  Concept concToGeneralize = cg1.getConceptWithType(carType);
  Type vehicleType = mainLexicon.getTypeCS(Identifier.wrap("Vehicle"));
  cg1.generalizeType(concToGeneralize, vehicleType);

The result of the code above:

cg1: [Drive] -
        -obj->[Vehicle],
        -agnt->[Human :imad]

Note: If, instead of Vehicle, we provided the identifier name Truck, generalizeType() will fail because Truck is not a superType of Car.

- generalize the designator of a concept in a CG: generalizeDesignator()

Let us assume the above CG cg1 with the goal to generalize the designator of the concept [Human: imad].

  Type humanType = mainLexicon.getTypeCS(Identifier.wrap("Human"));
  concToGeneralize = cg1.getConceptWithType(humanType);
  cg1.generalizeDesignator(concToGeneralize);

The result of the code above:

cg1: [Drive] -
        -obj->[Vehicle],
        -agnt->[Human]

- analogize the type of a concept in a CG: analogizeType()

Assume that CG cg1 is:

[Drive]-
     -obj->[Car],
     -agnt->[Man]

Assume also that the goal is to "analogize" the type of the concept [Car] to Truck, i.e. to replace the concept type Car by Truck if Car and Truck have a common superType (other than the ontology root type):

  Concept concToAnalogize = cg1.getConceptWithType(carType);
  cg1.analogizeType(concToAnalogize, truckType);

The result of the code above:

cg1: [Drive] -
        -obj->[Truck],
        -agnt->[Man]

Note: If, instead of Truck, we provided the identifier name Proposition and Proposition has no common superType with Car except the ontology root type, then analogize will fail.

- remove a concept from a CG: removeConcept()

System.out.println("\nThe CG copyOfCG1 (recall) :\n" +    

                            copyOfCG1.toString(mainLexicon));
copyOfCG1.removeConcept(concWater);

System.out.println("copyOfCG1 after the remove of [Water]:\n" + copyOfCG1.toString(mainLexicon));

The result of the code above:

The CG copyOfCG1 (recall) :
[Drink] -
    -agnt->[Man :imad],
    -obj->[Water]

copyOfCG1 after the remove of [Water]:
[Man :imad]<-agnt-[Drink]

- remove a relation with a specified type from a CG: removeRelation()

In general, a CG can content several relations with the same relation type. We use in the following example the method findRelations() that returns an enumeration over all relations of the CG that have the specified relation type. Then, we remove from the CG the first relation encountered in the enumeration.

cg1 = CG.parse("[Drive]-\n" +
                    "-obj->[Object],\n" +
                    "-agnt->[Person]", mainLexicon);
System.out.println("The CG cg1:\n " + cg1.toString(mainLexicon));

RelationType objType =

                mainLexicon.getRelationTypeCS(Identifier.wrap("obj"));
Enumeration objRels = cg1.findRelations(objType);

Relation objRel = (Relation) objRels.nextElement();
cg1.removeRelation(objRel);

System.out.println(

        "\nThe CG cg1 after the remove of the relation obj :\n" +
        cg1.toString(mainLexicon));

The result of the code above:

The CG cg1:
[Drive] -
    -obj->[Object],
    -agnt->[Human]

The CG cg1 after the remove of the relation obj :
[Drive]-agnt->[Human]

Examples of matching-based CG operations and other CG operations (like expand() and isCanonic()) are provided in CGOperations. See NewCGOperations for new CG operations. See also BindingContext for examples on CG unification.

See the Java class CGTest for a more complete view of the call/use of most of the methods of CG, see APIs Specification for the detailed specification of the CG API, CGOperations for detail on matching based CG operations, and Implementation Issues for detail on the implementation of CG API. Also, recall that Amine provides two GUIs related to CG: CGNotationsGUI for edition of CG according to their notations and to the languages used to express them, and CGOperationsGUI to apply and test CG operations.

CG vs Predicate

This section presents a theoretical discussion and comparison of predicate calculus and CG calculus. It can be skipped in a first reading.

What is the difference between predicate (calculus and logic) and CG (calculus and logic) ?, if they are equivalent and predicate logic is used by the majority, why using CG instead of predicate ?, etc. These questions are often rised when CG is compared to other knowledge representation schemes (predicate logic and especially KIF, Description Logic, Frame, etc.). Recently, the author was involved in an email discussion with Bernd Groh and John Sowa about these questions (see the CG List, during May 2004). Reader interested by the detail of the discussion may consult the CG Archives. The author reports here a synthesis of the discussion.

It is well established that CG logic is equivalent to first-order predicate logic, that CG is equivalent to KIF, etc. See John Sowa for detail about these equivalences. But what is the specificity of CG ?, why using CG instead of predicate ? The first and most mentioned reason is CG readability. Let us consider the following example, given by John Sowa, to illustrate this feature of CG:

Here is the proposition  Tom believes that Mary wants to marry a sailor  represented in CG:

[Person: Tom]<-Expr-[Believe]-Thme->[Proposition = 
             [Person: Mary *x]<-Expr-[Want]-Thme->[Situation = [Person ?x]<-Agnt-[Marry]-Thme->[Sailor] ]].

The same proposition, represented in Predicate calculus formula:

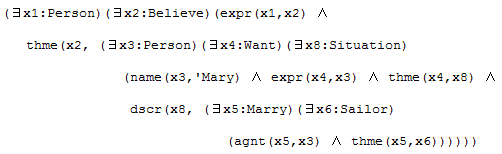
It is clear that CG is more readable and concise than predicate formulation.

Some reasons that make CG more readable than predicates are listed below:

1. CG notation uses less number of variables then predicate notation,

2. Connection between entities and predicates is explicit in CG; it is reflected by the graph structure of CG,

3. In CG logic, the chunk of information is a CG (which corresponds to a conjunction of predicates). In the predicate logic, it is a predicate. With CG, we think in terms of CG and operations on CGs. With predicate, we think in terms of predicate and operations on predicates. This difference in the "information unit" is very important and has a strong impact on the expressiveness (the expressive power or the abstraction level) of the notation and also on the operations and the processes that interpret the information.

4. When a description involves embeeded propositions, CG readability becomes hightly wanted !

The author argues that CG is not only more readable than predicates formula but CG has also a more expressive power than predicates formula. But what is the expressive  power of a language (like Pascal or Java) or of a notation (like CG or predicate) ? Expressiveness concerns the abstraction level of the semantic of the language or of the notation. It concerns the semantic constructs or categories that are provided to the user to modelize a description:
- With predicate calculus, human thinks/modelizes in terms of connectors, formulas, predicate structures, variables, scope, etc. He/She will be concerned by skolemization, transformation to Horn clauses, unification, etc.,
- With CG calculus, human thinks/modelizes in terms of concepts, relations between concepts, contexts, coreferences, type hierarchy, conceptual structures, ontology, matching-based operations, etc. These semantic constructs are more abstract than those of predicate calculus.

Thus, we can conclude from the above discussion that CG is more readable and more expressive (more abstract) than predicate. This difference between the two notations is relevant for human, but is it relevant also for computer ? some researchers suggest to use CG as a front-end notation for computer-human interaction. But for the computer, they suggest to translate CG in an equivalent predicates formula and then to treat this formula with predicate theorem proving and other predicate-based operations and processes. But this "reductionist" view neglects the fact that CG theory is not only the CG structure, it is also a set of CG-based operations and CG-based processes. In CG theory, CG is interpreted as such: CG is implemented as a graph, CG's operations are implemented as graph's operations, inference or any other process make use of CG directly, etc. Researchers in CG community developed algorithms that interpret CG directly. Amine Platform constitutes a good example of this approach: Amine provides both term/predicate (equivalent to predicate) and CG as two complex and basic structures (CG is not translated or reduced to a collection of terms). Amine provides a set of operations on term and another set of operations on CG, each set is defined and implemented according to the specificity (the semantic) of the structure in hand. See for instance the implementation of matching-based operations for both term and CG. Also, in CGOperations, we present two formulations for the algorithmic definition of CG matching-based operations: a) concept-centered formulation which interprets and exploits the graph structure of a CG, and b) relation-centered formulation which interprets a CG as a collection of relations (i.e. CG is translated to a collection of predicates). In CGOperations, we argue that the former formulation is more efficient than the latter. Efficiency aside, formulation of algorithms and codes that interpret CGs directly (as a graph structure and according to the semantic of CG theory) are more readable, more abstract and more easy to bear and to refine than equivalent algorithms that interpret predicates formula.

With this background, we can ask: why should we reduce and reformulate CG, Conceptual Structures, CG operations, and CG-based processes to predicates formula, predicate operations, and predicate-based processes ?

In addition, CG theory has its own logical foundation: Existential Graph (EG) Logic of S. C. Peirce which has been developed in parallel to Predicate Logic. See John Sowa for a detailed comparison of the two logics.

Appendice 1: Amine LF grammar

We use the EBNF notation to formulate LF and CGIF grammars: (X | Y) means category X OR category Y, (X)* means 0 or several occurrences of X, {X}* means 1 or several occurrences of X, [X] means that X is optional.

RLF1. CG  ::=  Concept  [Relation | Relations] .

RLF2. Concept ::= "[" Type  [":" Designator]   ["#" PseudoDesignator]   [CoReferent]    ["=" Descriptor]  "]" .

RLF3. Designator ::=  IndividualIdent | SetOfIndividualIdent | Variable .

RLF4. CoReferent ::=  ("*" | "?") Variable .

RLF5. Descriptor ::=  Amine_Object_Var .

RLF6. Relation ::= ("-" RelationType "->" CG) |  ("<-" RelationType "-" CG) .

RLF7. RelationType ::= RelTypeIdentifier |  TypeIdentifier | Variable .

RLF8.  Relations ::=  "-"  Relation  {"," Relation}*  [";"] .

A set of individuals can be an empty set or a sequence of individual identifiers, separated by comma ",".

RLF8. SetOfIndividualIdent ::=  "{"  [ IndividualIdent  ("," IndividualIdent )*  ]  "}"  .

RLF9. Type, RelTypeIdentifier, IndividualIdent  ::= Identifier .

RLF10. PseudoDesignator  ::=  {Character}* .

Variable and Identifier are defined in  Amine_Object_Var .

Appendice 2: Amine CGIF grammar

RCGIF1. CG ::= {Concept | Relation}*  .

RCGIF2. Relation  ::=  "(" RelationType Argument  Argument  ")" .

RCGIF3. Argument ::=  Concept | Designator  | PseudoDesignator .

Note: LF and CGIF use the same syntactic rules to formulate a concept.

Appendice 3: Grammar of Standard CGIF notation in Amine