Contexts, Canons and Coreferences
as a basis of a multi-paradigm language
Adil
KABBAJ
INSEA, Rabat,
MOROCCO, B. P. 6217
fax :
212 7 77 94 57
email :
akabbaj@insea.ac.ma
Abstract. This
paper shows how basic elements of CG theory, like CG structure, canon, context
and coreference constitute the basis of the
multi-paradigm language SYNERGY. For computational purpose, a) the definition
of coreference is extended to include ``compound coreference``, b) states and lifecycles are associated to
concepts and c) a finite set of data and control relations (in, out, guard,
next) are defined with propagation rules as their procedural semantic.
Computation model of SYNERGY
corresponds to a context activation mechanism which is based on concept’
lifecycle and relation’ propagation rules.
The preliminary version of the language has
been introduced in a previous paper [11]. Implementing and using the language
lead us to review, improve and complete its design. This paper presents the
result of such a work with an emphasis on the role of contexts, canons and coreferences in SYNERGY.
A companion paper [14] presents SYNERGY as
a concurrent object oriented language.
1. Introduction
Conceptual Graphs (CG) theory [23, 24] is
proposed as a graphic system of logic and as a formalism
for the representation of knowledge.
In programming language and system analysis,
graphs are used to describe sequential and/or parallel ``programs`` of
different kinds : procedural, process,
functional, event-driven, logical and object oriented programs [1, 15, 27, 28,
21, 16]. Moreover, various graph activation mechanisms have been developed as
computation models for the execution of the above kinds of programs-as-graphs.
The language SYNERGY, presented in this paper,
illustrates how CG formalism can be used as a multi-paradigm language, where
the above kinds of programs can be represented and integrated, using a minimum
of basic notions common to them all. Those notions correspond to the basic
elements of CG theory : CG structure, type
hierarchy, conceptual structures, context, canon and coreference.
For computational purpose, SYNERGY incorporates the following extensions : a) the definition of coreference
is extended to include ``compound coreference``, b)
states and lifecycles are associated to concepts and c) a finite set of data
and control relations (in, out, guard, next) are defined with propagation rules
as their procedural semantic.
Computation model of SYNERGY is based on a context activation mechanism, rather
than a logical approach with inference rules and some proof techniques. In
SYNERGY, computation is done in and with CGs without
the use of ``extra`` elements such as actors or the use of another
language/notation (like the approach taken by Lukose
for his Executable Conceptual Structures [17]).
Context activation in SYNERGY is
based on concept’ lifecycle and relation’ propagation rules. Concept’ lifecycle is similar to
process’ lifecycle (in process programming) and to active object’ lifecycle (in
concurrent object oriented programming), while relation’ propagation rules are
similar to propagation rules
(i.e. firing rules) in procedural graphs, dataflow graphs and
Petri Nets.
Different multi-paradigm languages have been
developed (for instance BETA [18], AKL [10] and Oz [22]). Also, different
formalisms have been extended to account for more and more programming
paradigms (as the case of Dataflow graphs [27, 20], Petri nets [8, 15] and
transition networks [21, 16]). In both categories, the difference concerns the
paradigms that are considered and the uniform
foundation that is used. What is specific to SYNERGY is its use of CG as a
uniform foundation for the integration of sequential and/or parallel
procedural, process, functional, event-driven and object oriented paradigms.
While a multi-paradigm language can be used as
a mono-paradigm language (by using only a subset of the language), it is in
fact more suited for applications that exploit different kinds of knowledge.
It should be noted that a multi-paradigm
language doesn’t involve necessarily ``a big and complex foundation``. This is
the case for instance of SYNERGY ; few basic
elements are used and one element can be used in different ways (as the case of
CG, context and coreference). The different uses of the same element constitutes a key feature of some
multi-paradigm languages.
SYNERGY is designed for visual modeling and
simulation. It can be used for different purposes and in many fields :
programming languages, simulation, database, information systems, software
engineering, knowledge acquisition, knowledge base systems, intelligent
tutoring systems and multi-agent systems. In [12] we reported the use of
SYNERGY in an intelligent tutoring system, especially for a visual
agent-oriented modeling of the Intensive Care Unit. In ``Programming
Languages`` course, the author uses SYNERGY to teach basic concepts of many
programming paradigms. SYNERGY is used also in an ongoing project concerning
the development of a multi-media environment for the design and simulation of
multi-agent systems.
SYNERGY, with its graphical environment, is
implemented on PC with Visual C++. An implementation on Silicon Graphics is
underway. The preliminary version of SYNERGY has been introduced in a previous
paper [11]. Implementing and using the language lead us to review, improve and
complete the design of SYNERGY. This paper presents the result of such a work
with an emphasis on the role of contexts, canons and coreferences
in SYNERGY.
The paper is organized as follows :
the first part of the paper (section 2) provides background information
concerning uses of conceptual graphs for procedural, functional and
object-oriented programming and also previous uses of the notion of context.
The second part of the paper (section 3) gives
an overview of SYNERGY, showing how contexts, canons and coreferences
constitute the basis of this language. Section 4 gives an example that
illustrates some aspects of
SYNERGY and section 5 summarizes the paper and suggests
directions for future work. The companion paper [14] presents SYNERGY as a
concurrent object oriented language and presents its use in a visual
agent-oriented modeling of the Intensive Care Unit.
2. Background
Section 2.1 reviews previous works concerning
the use of CG for sequential procedural programming, functional programming and
object-oriented programming. Section 2.2 reviews the works of Sowa [23, 26] and
Esch [4,5] about contexts.
2.1. Programming with
conceptual graphs
Conceptual graphs for
sequential procedural programming. Two examples are considered :
active semantic networks of
· While semantic networks have been
used mostly, in the seventies, for the representation of declarative
information, the group of
The evaluation (activation) of an active
semantic network (ASN) is based on a procedural activation mechanism which is
initiated by a request for an evaluation of a node X in an ASN [19] :
1.
Evaluate each argument
of X (if it can be evaluated). Replace the argument by its value.
2.
Follow the link
``act`` to locate the type of the node X.
3.
Transfer the argument
values to the corresponding parameters of the type.
4.
If the type of the
node X is related to a primitive with the link ``prim``
then evaluate the primitive
else evaluate the node Y which is related to X
with the link ``iswhen`` : X -iswhen-> Y.
/* link ``iswhen``
relates a type to its definition */
5.
If the node X is
related with the link ``then`` to a node Z : X
-then-> Z, then evaluate Z.
While active semantic networks were an important
step in ``programming with semantic networks``, at least three limitations can
be noted about them : 1) each new definition is added to the memory which
becomes a huge active semantic network without any modularization or context
mechanism, 2) the evaluation of a defined type involves the evaluation of the
definition itself (not a copy of it) and thus, a recursive definition or a
parallel evaluation of nodes with the same type are not possible, and 3) only a
restricted form of sequential procedures are considered.
SYNERGY uses also CGs
as active semantic networks, it overcomes however the above limitations by
exploiting the basic elements of the CG theory (like CG, context and coreference). Also, SYNERGY is a multi-paradigm programming
language ; it is not restricted to a form of
sequential programming or functional programming.
· Like
Conceptual graphs for
functional programming. In [25], Sowa illustrates how data flow diagrams, viewed as combinations
of functions, could be represented as CGs without
actors (functions are considered as relations). In [23], he considers a more
general form of dataflow diagrams, defined as combinations of actors, an actor can have one or several outputs (a function
could have only one output). As noted by Sowa in [25], dataflow diagrams by themselves
are not sufficient for a complete computational system ;
some control mechanisms are needed. Also, dataflow diagrams are graphic
single-assignment functional languages ; no
assignment that changes the value of a variable is permitted.
Dataflow diagrams with actors can be
represented as CGs by considering actors as concepts
(see Figure 1 for an example). With such a reformulation, it is no more
necessary to deal with two kinds of graphs (CG and dataflow graphs) and with CG
that contains concepts, actors and relations. The activation mechanism proposed
by Sowa for his dataflow graphs can be adapted to the CG reformulation.
We have considered such a reformulation during
the design of SYNERGY.

Figure 1 : An
actor viewed as a concept
Conceptual graphs for
object-oriented systems. Semantic networks with some programming languages, like Simula, have inspired the development of object oriented
languages. In CG community, works have been done to map object-oriented
concepts in CG [9, 29] and to use CG as a logical foundation for object-oriented
systems [26, 3]. For the representation and interpretation of methods, Hines
and al. proposed actor graphs, Ghosh and Wuwongse proposed schemata with actors, Sowa proposed a
rule-like formulation and Ellis proposed a state based approach. In SYNERGY,
both the descriptive part of a class and its methods are represented by CG. CG
activation mechanism is used to execute a method.
Discussion of the above approaches is given in
the companion paper [14], as well as the concurrent object-oriented model embedded
in SYNERGY.
2.2. Some uses of
contexts
In [26], Sowa uses contexts to formulate type
definition and instance description. For example, instead of the statement type CAR(*c) is CG, Sowa formulates the definition
as a concept : [CAR : *c CG].
An instance is described in the same way :
[CAR : PCXX999 *c CG].
This approach has been adopted in SYNERGY too
(i.e. the use of context to describe conceptual structures).
Let’s consider now the relationship between
context and concept. Esch [4, 5] considers contexts
and concepts as abstraction duals. In effect, the definition of a type must be
true of every instance of the type. Thus, a concept like [CIRCUS-ELEPHANT : *x] is just an abstraction of a more
detailed formulation which states explicitly that the definition of
CIRCUS-ELEPHANT is true of *x :
[CIRCUS-ELEPHANT : *x] =
[CIRCUS-ELEPHANT : *x [ELEPHANT :
*x]<-(AGNT)<-[PERFORM]->(LOC)->[CIRCUS] ]
The right side of the equality is a context
that represents the ``white box view`` of the concept in the left side [4, 5].
A similar result is obtained for a referent that has an individual description : the concept
[CIRCUS-ELEPHANT : Jumbo] is just a ``black box view`` (an abstraction) of
the context where a more precise description is given ; [CIRCUS-ELEPHANT :
Jumbo CGJumboDescr
].
Esch [5] defines an operation that changes a
concept to a context, i.e. it changes a concept from the ``black box view`` to
the ``white box view``. The operation, called referent expansion (REFEXP) expands a
concept’ referent (by copying its defining graph). He defines also its reverse ; referent
contraction (REFCON).
Referent expansion has been used implicitly by
Sowa [26] : in step four of his method’ execution
and concerning the concept/method [START-ENGINE] that is contained in the
description of the car PCXX999, Sowa states to ``initialize the description of
the START-ENGINE box by copying the definition of its type``.
The hypothesis of ``contexts and concepts as
abstraction duals`` and the referent expansion operator are fundamental to
SYNERGY.
3. An overview of SYNERGY
Sections 3.1-3.3 present the use of canon,
contexts and coreferences in SYNERGY. Sections 3.4 and 3.5 concern the computation model of SYNERGY, i.e.
the context activation mechanism and the SYNERGY interpreter that manages the
parallel activation of contexts.
3.1. SYNERGY’ program
is a canon
Sowa introduces canon as a formal definition of a knowledge base. A canon consists
of four components [23 p.96] : a type hierarchy,
individual markers (instances), conformity relation which relates an instance
to its type and a finite set of CGs, called canonical basis. Sowa notes that
canonical basis can be simple (just a set of axioms or a set of primitives
actions) or it can be very large (i.e. containing background information like
types definition, instances description, schemata, etc.).
Esch [6] proposes the following equation :
Canons = Contexts + Individuals + Types. The canonical basis of such a canon is
composed of types definition, instances description
and assumptions or axioms. Esch describes a canon as
a labeled context. To have a more uniform formulation of a canon, its
components (type hierarchy, conformity relation and definitional statements)
should be expressed also with CG notation. In this sense, Esch
[6] notes that conformity relation can be specified as a concept that is
considered as a canonical graph. For instance, canonical graph is [CIRCUS-ELEPHANT :
Jumbo] states that Jumbo is conform to the type CIRCUS-ELEPHANT. Also, the type
hierarchy can be specified as a CG [25, 6] and as noted above, Sowa [26] uses
contexts to specify type definition and instance description.
A ``program`` or an application in SYNERGY is a
canon composed of a type hierarchy, a conformity relation and the canonical
basis which contains types definition, instances description and schemata. A
canon is described as a context and its components are described as CGs.
Beside the canon which is considered as a base
where knowledge about a domain (or some related domains) is stored, SYNERGY
provides a ``working space`` where the user specifies his requests. Requests
are CGs that can be evaluated (executed) in parallel.
In SYNERGY, the canon and the working space are
called ``Long Term Memory`` and ``Working Memory`` respectively. The two are
described as two concepts : [LTMemory :IdentLTM CGKB] and [WorkingMemory :IdentWM CGsRequests]. The description of a canon (i.e. CGKB) is a taxonomic hierarchy (a hierarchy of types definition and instances description) augmented with
situations (schemata). The hierarchy is described as a CG with three types of relations :
[TYPE1] –subtà
[TYPE2] :
TYPE2 is a subtype of TYPE1 ;
[TYPE1] –instà [TYPE1 : InstanceName] : InstanceName is an
instance of TYPE1 ;
[TYPE1] –scmà [SCHEMA : Schema1] : Schema1 is a schema for TYPE1.
If a type TYPE1 is defined, its definition is
specified in the referent of the concept [TYPE1]. If an instance InstanceName has a specific description, this later is
specified in the referent of the concept [TYPE1 :
InstanceName]. In the same way, the description of a
schema Schema1 is specified in the referent of the concept [SCHEMA : Schema1]. By clicking
on a concept, a user can zoom in to see the details of the referent. This is
true for the canon itself since it is described as a concept with the
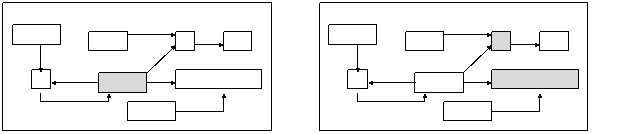
above hierarchy in its referent. Figure 2 illustrates the zoom in the canon
(i.e. the concept [LTMemory : ...]) as well as the zoom in the concept
[Nurse :_n] that is contained in the canon.
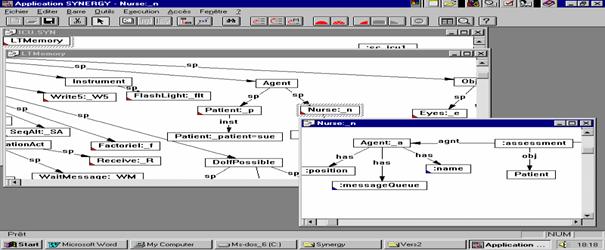
Figure 2 : A
portion of a canon with a zoom in a concept
In SYNERGY, the canon is used according to a
``programming`` view (not a logical and axiomatic view). Thus, for every new
application, SYNERGY provides ``the built-in canon`` which is composed of primitives
types and predefined types (defined in SYNERGY but provided to the user as
primitive). The user can extend the built-in canon by defining new types and
instances and by describing new schemata.
Figure 3.a gives the definition of a new type
IS_ADULT which is a subtype of the primitive type STRICT_PROCEDURE. Thus,
IS_ADULT is added to the canon as a procedure with strict evaluation. Figure
3.b illustrates how the user can specify and add to the canon instances of
types, either by giving an explicit description of the instance (as for MyTable in Figure 3.b) or just by specifying that the
individual is an instance of a type (as for Tble34).

(a) (b)
Figure 3 :
Definition of a type and description of instances
As noted before, the built-in canon is composed
of primitives and predefined types. Among primitives types, SYNERGY provides
basic data types (INTEGER, STRING, BOOLEAN and WINDOW), basic operations
(assignment, arithmetic, relational, boolean,
list, I/O and window operations), CG structure and a large set of CG operations
(Unification, Maximal join, Generalization, Subsumption,
Contraction, Expansion, etc.). Communication operations for concurrent
object-oriented programming (like Send, SendSync,
Receive, WaitMessage, etc.) are examples of
predefined types.
Four primitives types are of interest :
PROCEDURE_ACTIVITY, PROCESS_ACTIVITY, STRICT_ACTIVITY and LAZY_ACTIVITY. They
are subtypes of the primitive type ACTIVITY. PROCEDURE_ACTIVITY and
PROCESS_ACTIVITY reflect the difference in the life-time of an activity while
STRICT_ACTIVITY and LAZY_ACTIVITY reflect the difference in the evaluation mode
of the arguments of an activity (if it has arguments). The user can specify
some of those primitives as super-types of a new defined type and so, the new
type will be interpreted according to the semantic of the super-types. For
instance, if the type of a concept C is a subtype of PROCEDURE_ACTIVITY and the
concept C has a description, then after its activation, the description will be
destroyed. Thus, each activation of the concept C involves the creation of a
new description, this is similar to the creation/destruction of procedure’
record activation in procedural programming. However, the description of a
concept-process (i.e. the type of the concept is a subtype of PROCESS_ACTIVITY)
will not be destroyed after its activation.
Remarks : In [25,26], Sowa considers
several types of activity (i.e. action, procedure, process) as concepts except
a function which is treated as a relation. For uniformity purpose and
especially if CG is used for doing computation, it should be better to consider
functions also as concepts (i.e. a function is a kind of activity !).
3.2. CG of SYNERGY
Concept. In SYNERGY (as in [26, 4, 5, 6]), a concept can
have a referent with a description. A referent, when specified, can be an
instance name, a variable or a coreference. The
description of a referent can be a data type or CG(s). In addition, a concept
has in SYNERGY a state and a lifecycle. Concept’ lifecycle is a state
transition diagram where states correspond to the possible states of a concept.
Concept’ lifecycle (including
concept’ state), along with relation’ propagation rules, constitute the basis
of SYNERGY’ computation model. They are considered in section 3.4.
Relation. Only dyadic relations are considered in SYNERGY (they are the most
used). The language provides a finite set of ``built-in`` relations subdivided in : 1) data relations (in and out), 2) control
relations (guard ``grd``
and next) and 3) memory relations (subt, inst, scm)
introduced above.
Data and control relations (in, out, grd, next) as well as coreference
links have a special status in SYNERGY since they have a procedural semantic
(i.e. defined as propagation rules, presented in section 3.4) that influences
the context activation process. The user can use other relations but they have
no effect on context activation.
¨ C1 -in-> C2 specifies that the concept C1 is an input
argument of the concept C2 (C2 could be a procedure or a function for example).
¨ C3 -out-> C4 specifies that the concept C4 is an output
argument of the concept C3.
¨ C1 -grd-> C2 specifies that the concept C1 is a condition
for C2 : the description of C2 cannot be determined and activated unless
the description of C1 is determined, activated and it is different from
``false``. The relation ``guard ; grd`` can be used to express a ``boolean
condition`` or a ``synchronization condition`` (if, for instance, an
action C2 can be done only if the action C1 is done).
Guard relation ``grd``
is more general than the relation COND used by Sowa [25] and which corresponds
to the conditional in KIF and to the MERGE (or SELECTOR) actor in dataflow
graphs [2, 7] : (COND
Condition Arg2 Arg3) ; COND returns the value of Arg2
if Condition is true and the value of Arg3 otherwise. COND is useful for
functional programs only, while guard relation can be used to express
conditional in different paradigms (i.e. functional and procedural paradigms).
Multiple-assignment and procedural interpretation
of ``in``, ``out`` and ``grd`` relations are
considered by default in SYNERGY : for C1 -in-> C2 or C3 -grd-> C4, an access to the description of C1 (or C3)
will not involve its consumption, and for C5 -out-> C6, C5 can assign a new
description (value) to C6 even if it has already one.
Functional interpretation of the above three relations will be adopted however, if the user
post-fixes the relation name with the optional attribute ``f`` : for C1 -in,f-> C2 or C3 -grd,f-> C4, the description of C1 (or C3) will be
consumed just before the activation of C2 (or C4), and for C5 -out,f-> C6,
C5 can assign a new description to C6 only if it has not, otherwise C5 will
wait for the consumption of C6’ description.
¨ C1 -next-> C2 specifies that the concept C2 will be
triggered after the activation of C1. But, contrary to the relation ``grd``, the activation of C1 isn’t a condition for C2.
3.3. Context, coreference and coreference
resolution in SYNERGY
In the CG theory, the concept with referent *x
indicates the first occurrence or the defining
node of the variable x while a concept with referent ?x
is a bound node and indicates a
subsequent reference to the concept where the variable is defined [25]. The
pair (*x, ?x) shows a coreference
link between coreferent concepts. Esch
[6] has noted that ``the basic thing to remember about contexts and coreference is that it closely models scope of variables in
block structured languages``. Indeed, a variable can be defined in a procedure
and referenced in another procedure, the two
procedures correspond to labeled contexts.
In SYNERGY, the pair (r, r.) is used instead of
(*r, ?r). For computational purpose and to
enhance the expressive power of the language, SYNERGY provides a new kind of coreference called compound
coreference ``r1.r2. ... rN`` where ``rj`` is the
referent of a concept (or the label of a context). Compound coreference
enables a specification of a coreference link even if
the defining node isn’t present at the time of the specification. Let’s
consider for example the following situation (Figure 4)
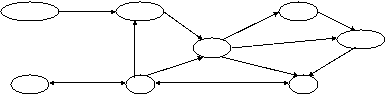
: the bound node [BOOLEAN : Daniel.Eyes.CanOpen]
is a compound reference to a concept [BOOLEAN : CanOpen]
that should be nested in the context/concept [EYES : Eyes] which should be
nested itself in the context/concept [MAN : Daniel].
![]()
Figure 4 :
Compound coreference
To determine the description of the bound node
[BOOLEAN : Daniel.Eyes.CanOpen],
the language’ interpreter should resolve
the coreference, i.e. it should identify its
defining node. Resolution of a compound coreference
assumes the hypothesis of ``contexts and concepts as abstraction duals`` and
the ``referent expansion operator``. For our example, the concept [MAN : Daniel] is localized and its referent is expanded
(by copying its defining graph) as well as the referent of the concept
[EYES : Eyes] (Figure 5). This later contains the defining node ; a concept with the referent ``canOpen``.

Figure 5 :
Resolution of a compound coreference
In SYNERGY, when a user clicks on a bound node
to have its description, he will get the description of the associated defining
node (if it has a description), since a bound node is only a reference to its
corresponding defining node.
Coreference and its resolution are used in
SYNERGY to implement inheritance for object-oriented programming :
a class inherits attributes of its super-class (and so on recursively). The
defining graph of a class C should contain a concept that ``represents`` its
super-class : [SuperOfC :
super]. When a reference is made to an attribute of an object (i.e. an instance
of the class C) and the attribute is not in the object description, a search
for the attribute is done in the object’ super-class, i.e. in the description
of the concept [SuperOfC : super] and so on recursively.
Example :
The type NURSE is defined as a subtype of the
type AGENT and it contains in its definition the concept [Agent
: super] (Figure 6.a). Let’s assume now the following situation (Figure
6.b) : a context C contains the concept [Nurse :magy] and there is a context embedded in the context C that
contains the concept
[Window :magy.window] which assumes that
“window” is an element in the description of “magy”.
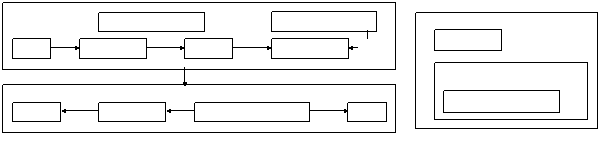
If the description of [Window
: magy.window] is requested, then the compound
coreference ``magy.window``
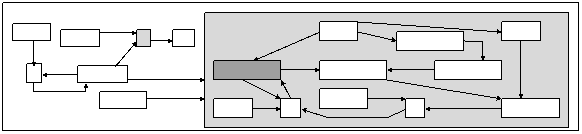
must be resolved : the concept [Nurse :magy] is
localized, its description is then determined (by referent expansion) (Figure
7) and the concept with referent “window” is looked for in the context of
[Nurse :magy].

Figure 7 :
Referent expansion
The concept is not found in magy’description
but this later contains a ``super-concept`` (a concept with referent
``super ``) [Agent : super], hence the search
will continue in the context of the super-concept, once its description is
determined (by referent expansion) (Figure 8). This new context contains a
concept with “window” as referent.
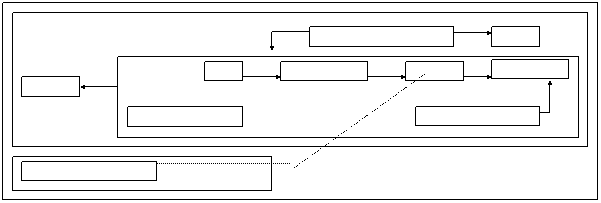
Figure 8 :
Inheritance by referent expansion and coreference
resolution
Related to inheritance and object-oriented
approach is the notion of ``self``. A reference could be made, in the defining
graph of a class C, to an attribute of a subclass of C. Examples are given
below, after the definition of the coreference
resolution procedure.
To define the coreference
resolution procedure, the notion of ``active context hierarchy`` should be
defined first.
Active context hierarchy is a hierarchy of contexts that are active during a ``program``
execution. The root of this hierarchy is the canon (i.e. the long term memory)
with the working memory (WM) as a direct ``descendant``. Each active concept of
the WM such that the description of the concept’ referent is a CG, constitutes
a direct descendant context of the WM context, and so on, forming a hierarchy
of active contexts. Contexts are added to and/or deleted from the hierarchy
during the execution of the ``program``.
Coreference resolution procedure searches, in the active context hierarchy, the defining node of a bound
node. There is basically two cases :
n
Resolution of a simple coreference [T : r.] that is immediately nested in the
context C (C is a node in the context hierarchy). The resolution of the coreference ``r.`` is
realized by a search that begins with C, then the father-context of C and so on
until a concept with referent ``r`` is localized in the current context or the
root-context of the hierarchy is reached.
n
Resolution of a compound coreference [T : r1.r2. ... .rN] begins with the resolution of ``r1.`` as
described above. Once the concept with referent ``r1`` is localized and its
description determined (by referent
expansion if necessary), a new search begins : the resolution procedure
looks for a concept with referent ``r2`` in the description of r1, then the
description of ``r2`` is determined and the procedure will look for a concept
with referent ``r3`` in the description of ``r2``, and so on for every ``rj`` of the compound coreference
until a concept with referent ``rN`` is localized in
the description of ``rN-1``.
The above basic treatment is
modified to take into account inheritance and
``self`` :
n
Assuming the above treatment for the resolution of [T :
r1.r2. ... .rN], when a
concept with referent ``rj+1`` cannot be localized in the context labeled by ``rj``, the coreference resolution
checks first if the context of ``rj`` contains a super-concept (i.e. a concept with
``super`` as referent). If so, the coreference ``rj+1.rj+2. ....rN`` is replaced by
``super.rj+1.rj+2. ....rN`` and then the coreference resolution is resumed. By adding the special
referent ``super``, the search is directed to the context of the super-concept,
implementing in this way the inheritance mechanism.
n
A reference [T : self.r1.r2. ... .rN] could be made in the context of
a super-class of an object. To resolve such a coreference,
the resolution procedure downwards the super-classes of the object towards this
later (see the example below).
Example :
To illustrate coreference
resolution, let’s consider the following situation (Figure 9) and especially
the three cases (a), (b) and (c). For each case, we specify in Figure 9 the
bound node (the input of the resolution procedure) and its defining node (the
output of the resolution procedure) :
à case (a) is about the bound node [Tr :
mr.] which is in the context [T :rfa = ...]. The
resolution procedure begins with a search of a concept with referent ``mr`` in the context [T :rfa = ...].
This later, as well as its super-concept don’t contain such a concept, the
search will then continue with the ``father-context`` :
[Type : _X = ...]. This later
doesn’t contain a concept with referent ``mr`` but it
contains a super-concept [T2 : super = ...].
Hence, a search will continue in this context. Again, the search fails in the
current context and it will continue in the context of the super-concept ; [T4 : super = ... ]. This later contains a concept with
referent ``mr`` and so, the defining node for [Tr :
mr.] is found.
à case (b) is about the bound node [Tb : self.titi] which is in the context [T5 :super = ...]. In its downward search (Figure 9
should be visualized in 3-D), the resolution procedure ignores the contexts of
the super-concepts [T5 :super = ...], [T4 : super =...] and [T2 :
super =...]. The concept/context [Type : _X =...]
is then considered. This later, as well as its super-concept don’t contain a
concept with referent ``titi``, the search will then
continue with the ``father-context`` : [TypeA : _A =
...] which contains the concept [Tb : titi]. The
defining node for [Tb : self.titi] is thus
found.
à case (c) is about the bound node [Tc :
self.tata] which is in the context
[T5 :super = ...]. This case is
similar to the precedent but it illustrates an important point :
contexts of the super-concepts [T5 :super
= ...], [T4 : super =...] and [T2 : super =...] are ignored
and the search fails in the context of [Type : _X =...] but it succeeds in
the context of its super-concept [T2 : super =...] where the defining node
[Tc : tata] is
specified. The context [T4 : super =...] contains also a concept with referent
``tata`` but the context [T2 : super =...] is
considered first, hence it has priority over the context [T4 :super =...].
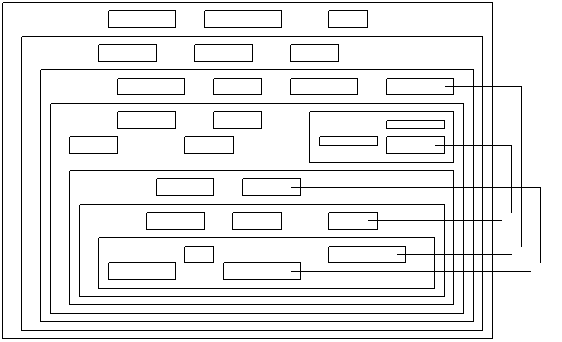
Figure
9 : Examples of coreferences
resolution
A more detailed description of coreference resolution, where other cases are considered,
is given in [13].
In SYNERGY, coreference
is not only an abstraction mechanism, it effects also
the context activation mechanism, as data and control relations do. This aspect
is considered in the next section.
3.4. Context
activation = Relation’ propagation rules + concept’ lifecycle
The activation of a SYNERGY’ application begins
with the activation of the working memory ; the
first active context. A context activation corresponds in general to the
activation of its description ; a CG or a set of CGs.
Activation of a CG begins with the parallel activation of some concepts of the
CG, then data and control relations (if they are present) spread the activity
through the graph.
Concept’ activation is done according to the
concept’ lifecycle while the spreading activation is conform to relations’
propagation rules. The propagation rules are defined first
and then the concept’ lifecycle.
Relation’ propagation
rules
An activation of a concept C is initiated in
general by putting the concept in the state ``trigger ; ?``.
This state means that the concept is
requested to determine its description and then to execute it. Data and/or
control relations connected to the concept C will propagate the request, if
some conditions are satisfied, to concepts related to C. A relation can
propagate the request forward (from the source to the target of the relation)
and/or backward (from the target to the source of the relation).
The following propagation rules
apply for data and control relations as well as for coreference
link (viewed as a relation between a bound node and its defining node : C1 –corefà
C2).
Forward propagation
rule
If an active context, described by CGs, contains a branch C1 –Relà C2 where Rel Î {"in", "out",
"grd", "next", "coref"}and if C1 has
responded to the request ``determine and then execute your description`` (and,
if Rel = ``grd``, the
description of C1 is different from ``false``), then the relation Rel will propagate forward the request to the concept C2.
Backward propagation
rule
If an active context contains a branch
C1 –Relà C2 where Rel
Î {"in", "out",
"grd", "coref"}and
C2 is requested to ``determine and then execute your description`` and
n
if Rel =
``in`` and the type of C2 is a strict activity (i.e. C2 description cannot be
executed if one of the input arguments of C2 hasn’t a description) and if C1 is
at state ``steady ; o`` and hasn’t a description, then the relation Rel will propagate the
request backward to C1, i.e. C1 will become at state ``trigger ; ?``.
n
if Rel =
``out`` or ``coref``, and C2 hasn’t a description and
its type isn’t defined (i.e. the description cannot be determined by referent
expansion operator), then the
relation Rel will propagate the request backward to
C1.
n
if Rel = ``grd`` and C1 is at state ``steady ; o`` and hasn’t a
description, then the relation Rel will propagate the request backward to C1.
Forward and backward propagation
role of a relation Rel can be inhibited if the
optional attribute ``/`` (Rel,/)
and ``\`` (Rel,\) is specified, respectively. For
instance, if an active context contains C1 –in,/à
C2 and the concept C1 has responded to
the request ``determine and then execute your description`` then the relation
``in,/`` will not propagate the request to the concept C2.
With the attributes ``/` and ``\``,
the user can control the propagation of concepts’ activation in a context C.
This is similar to the use of the ``cut`` to control the backtracking in
PROLOG. We refer the reader to [13] for more details about this point.
Concept’ lifecycle
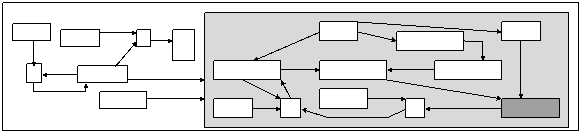
Concept’ lifecycle is a state
transition diagram (Figure 10) where states correspond to the possible states
of a concept and transitions to the conditions/actions on the concept and its
context (especially data and control relations linked to the concept). A
general description of concept’ lifecycle is given first and then a more
detailed description.
Possible states of a concept :
o : steady state,
 ? : trigger state,
? : trigger state,
@prc :
check-preconditions state,
@prc@ :
wait-preconditions state,
@ : wait-value state,
!@ : in-activation state,
@aft : wait-affectation state,
@nda :
wait-end-affectation state.
Figure
10 : Concept’ lifecycle
A concept C at state ``trigger ; ?`` is requested to ``determine and then
activate (i.e. evaluate or execute) your description``. Once the description is
determined, if the concept C has preconditions, it will enter a waiting phase
until its preconditions are satisfied. At the end of this waiting phase, the
concept’ description is evaluated and then, the concept will enter another
waiting phase until its post-conditions are satisfied. After that, the concept
C will become at state ``steady ; o``.
Let’s consider now the concept’
lifecycle in more detail : to determine the description of a concept C, three
cases are possible : a) the concept C has already a description or the
type of C is a primitive operation and so the description corresponds to a
primitive’ call, b) the type of C is defined and hence, the description is
determined by copying the defining graph (referent expansion operator), or c)
the description of C should be computed ; initiate a backward propagation,
through relations ``out`` and/or ``coref``. If the
later case occurs, the concept C will change its state to ``wait-for-description ; @``. C can stay indefinitely in the state
``@``. However, as soon as the description of C is determined, C becomes again
at state ``trigger ; ?``.
Preconditions for a concept C are
expressed with links of type ``in`` (X –inà C) and/or ``grd``
(Y –grdà C). If C is at state ``trigger ; ?`` and it has a description and has
precondition links, then the backward propagation rule of these links is
applied in general and C will change its state to ``check-preconditions ;
@prc``. Concepts that are sources of the precondition
links are then considered and the concept C becomes and stays at state
``wait-for-preconditions ; @prc@``
until all its preconditions are satisfied.
If the concept C hasn’t preconditions
or if they are satisfied, then its description is activated in parallel to the
other active concepts and C becomes at state ``in-activation ; !@``.
If the description of C is a CG then it is activated recursively, if it
corresponds to the call of a primitive then it is executed, otherwise (i.e. the
description is of a basic data type like integer or boolean) the activation is ``null``, i.e. it takes no
time and it has no effect.
If the activation of the description
is terminated and the concept has post-conditions, then they are considered.
Three kinds of post-conditions are possible :
n
Assignment of values computed by the concept C (if its description
corresponds to the call of a primitive with output arguments). If C is related
to one of its output argument C1 with a functional ``out`` relation (C –out,fà C1) and C1 has already a description (a value),
then C will change its state to ``wait-for-affectation ; @aft``.
n
Even if all the values computed by C can be assigned to the corresponding
output arguments, C can still wait due to a ``conflict of affectations`` which
occurs when several concepts attempt, at the same time, to affect values to the
same concept. In this case, C will change its state to ``wait-for-end-of-affectation ; @nda``.
n
If the concept C has terminated its activation and has satisfied the
above assignment’ post-conditions (if it has) and if it is related to a concept
C1 (C –Relà C1) with Rel
Î {"in", "out",
"grd", "next", "coref"}
without the attribute ``/``, then the forward propagation rule of Rel is applied.
Once all the post-conditions of the
concept C are treated, C will become at ``steady state ;
o``.
The graphical environment of SYNERGY
uses specific icons and colors to specify states of a concept. For instance,
when the state of the concept is `` trigger ;
?``, the color of the rectangle that represents the concept is green (it
becomes red when the concept is in-activation) and when the concept is at state
``@``, a triangle is placed at the left of the rectangle. With this
visualization, the user can see the
evolution of the interpretation of each concept.
To summarize this section, activation of a
context corresponds to a parallel activation of some of its concepts,
each concept is activated according to its lifecycle. A concept can be itself a
context, or it can be a primitive. Thus, the
interpreter should manage the parallel activation of several contexts and
several primitive calls.
The association of a
state to a concept is the main reason that makes such a parallelism possible.
In effect, each concept is interpreted (i.e. evolves, changes) according to its
lifecycle, the activation (or interpretation) of the context is thus
decentralized.
The following section describes how SYNERGY’ interpreter
manages the parallel activation of several contexts and several primitive
calls. In other words, it shows how the interpreter simulates a parallel
interpretation of concepts’ lifecycles.
3.5. SYNERGY
interpreter = parallel activation of contexts and primitives
This section gives a general description of
SYNERGY’ interpreter, more detail is given in [13].
The inherent parallelism of SYNERGY is realized
by the main loop of the interpreter. Indeed, at each
iteration all the active contexts (i.e. CGs)
and primitive calls are considered and, for each active context, all the
concepts that should be treated are considered too. The main loop is executed
until there is no more activity in the working memory context (which is the
first active context). This condition becomes true only if there is no active
context and no primitive in-execution.
The body of the main loop reflects
the composition of the concept’ lifecycle (this is expected since the
interpreter simulates a parallel interpretation of concepts’ lifecycles) : the first part of the loop concerns the left part of the
concept’ lifecycle (if the state ``!@`` is considered as the center (Figure
10)) and the second part concerns the right part.
First part of the loop : for every active context, interpret
every concept with state ``trigger ; ?``, then every concept
with state ``check-preconditions ; @prc`` and
then activate every concept that is ready for activation and set its state to
``in-activation ; !@``.
Second part of the loop : two procedures are called in this part : CheckEndActivationOfPrimitives
and CheckEndActivationOfContexts, that check if any
active concept has terminated its execution, if so the concept’ post-conditions
are considered.
Let’s consider now how the
interpreter treats parallel concepts’ activation (i.e. parallel activation of
contexts and primitives). Two global variables are used for this effect : the list of active contexts (LActiveCtxts) that implements the ``active
context hierarchy`` and the list of active primitives (LPrimitivesInExec). At each
iteration of the main loop, elements can be added and/or eliminated from
the two lists. For instance, an element will be added to one of the two lists
if a concept changes its state to ``in-activation ; !@``
and if its description is a CG or a primitive call.
The list of active contexts (LActiveCtxts) serves two purposes :
it indicates to the interpreter the active contexts that should be interpreted
in parallel and it allows the resolution of coreferences.
An element of this list contains information used to interpret a context. The
list LActiveCtxts is initiated with two elements, the
first for the long term memory LTM (the canon) and the second for the working
memory WM. Each element of the list refers to its ``father`` (since the list
represents a hierarchy).
The list of active primitives (LPrimitivesInExec) serves to simulate the parallel execution of primitives calls since the target machine is sequential (for
the moment). In effect, SYNERGY differentiates between ``physical`` and ``conceptual``
execution of a primitive, and between ``physical cpu-time``
and ``conceptual SYNERGY unit-time`` which corresponds to a main loop
iteration. Indeed, for the interpreter, what is done in one main loop iteration
takes one SYNERGY’ unit-time. Thus, a primitive that is really executed in Tp cpu-time is viewed by the
interpreter as if its execution takes Ts iterations (i.e. Ts SYNERGY unit-time), with Ts = Tp / Cste, Cste
is a constant fixed at start.
Hence, when a concept changes its
state to ``in-activation ; !@`` and its
description corresponds to a primitive call, this later is immediately executed
(the physical execution) and its ``physical cpu-time``
Tp is determined. The two are then converted to
the SYNERGY view : an element E is added to the list LPrimitivesInExec, the element E records information
like the values computed by the primitive (if any) and its ``SYNERGY-time`` Ts.
While the element E is in the list LPrimitivesInExec, the primitive is considered by the
interpreter as in-activation (this is the ``conceptual execution``). After each
main loop iteration, Ts of each active primitive is decreased by one until Ts = 0, in which case the interpreter
assumes that the primitive has finished its execution.
Conceptual parallelism vs physical parallelism
The above
discussion leads us to precise the difference between conceptual parallelism and physical
parallelism. As a parallel language, SYNERGY allows the user to write
parallel programs, its interpreter is able to execute those programs and its
graphical environment allows the user to
see their parallel activation. This ``conceptual parallelism`` is at the
design and the language level, it can be implemented on a parallel machine
(i.e. physical parallelism) or interpreted and simulated on a sequential
machine. In our current implementation of SYNERGY, we have considered the
second case. Of course, some constraints have been assumed, especially for primitives parallel execution. For instance, we assume that
during the execution of a primitive, no interaction could occur between the
primitive and the other parts of the ``program``. Our simulation of primitives’
parallel execution is based on this assumption. A primitive that doesn’t
respect the above constraint should be defined in SYNERGY.
4. Example
Assume that the following request is
contained in the working memory (Figure 11.a) :
the concept [Int =3] is at state
`` trigger ; ?``, the relation ``in1`` propagates this
activation to the concept [+] (Figure 11.b).
![]()
Note : in diagrams, a rectangle with a ``colored surface`` represents a concept with state ``trigger ; ?``.

Figure 11 :
Execution’ steps for the example
The activation of [+] produces a new
value for the concept [Int =10] which becomes [Int =13 # ?] (Figure 11.c). Next, the two concepts [*] and [HeaterSystem] are triggered and then activated in parallel
(Figure 11.d).
Note the use of the attribute ``/``
to prevent a propagation of activation through the relation ``in2`` ([+] ßin2,/--
[Int = 13 # ?]) and in this way, to prevent a
cyclic activation of [+].
The description of the concept [HeaterSystem] is determined (by referent expansion ;
copying the defining graph of the type HeaterSystem
which is defined in the long term memory) and then activated (Figure 11.e). The
activation of this context begins with the concept-parameter [Temp :in1/] which is in coreference
with the concept [Int =13] (a concept-parameter,
identified by the prefix inX/ or outY/
in its referent, is in coreference with its
corresponding argument).
HeaterSystem is about the heater of a room that
has a thermostat and a temperature. The goal of the heater is
to increase the temperature until it becomes equal to the value of the
thermostat’ switcher. This goal is satisfied by a cyclic behavior : the system checks, at each iteration, if the
temperature is less than the switcher’ value. If so, the heater’ state is set
to ``on`` and so, it initiates an increase of the temperature (by 1 in our
case). The change in the temperature will initiate another
iteration (check again if the temperature is less than the switcher’
value, etc.) and so on until the temperature is equal to the switcher’ value.
In that case, the heater’ state will be set to ``off`` and thus, one condition
to activate an increase of the temperature is not hold (Figure 11.e).
![]()
The activation is then propagated
through the relation ``in1``, from [Temp :in1/]
towards the concept [CheckTemp] (Figure 11.f).

![]()
Next, the description of the concept
[CheckTemp] is determined (by referent expansion) and
then activated. The defining graph of CheckTemp is
defined below : it specifies that if the value of
the temperature is less than the value of the switcher, then the value ``on``
is assigned to its output (the State of the heater), otherwise the value
``off`` will be assigned :
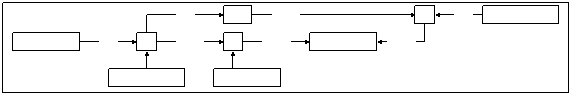
Once the activation of the
description of the concept [CheckTemp] is terminated,
the description is erased since the type CheckTemp is
defined as a subtype of PROCEDURE_ACTIVITY. The activation is then propagated
from [CheckTemp] towards the concept [State =on]
(Figure 11.g). Note that during the activation of [CheckTemp],
the concept [*] that is contained in the upper context (the context of Exple1)
has terminated its activation and produced a value (26) for its output
argument.
![]()
The activation is then propagated,
from the concept [State =on] towards the predicate [=]. This
later returns ``true``. Since this predicate is a guard for the concept
[+] ( i.e. [=]—grdà[+]
) and it is true, [+] is activated and it produces a new value (i.e. 14) for
[Temp :in1/] and [Int = 13]. This change of the
value initiates a new activation of both, [*] in the upper context, and [CheckTemp] in the context of [HeaterSystem].
Note that this change doesn’t activate the concept [+] since the relation ``in1``
has the attribute ``/`` ( [Temp :in1] –in1,/à[+]
).
As for the precedent iteration, the
description of [CheckTemp] is determined (by a new
copy of its defining graph) and then activated. Since 14 < 15 (14 is the
current value of the temperature and 15 the value of the switcher), [CheckTemp] sets again the heater’ state to ``on``,
involving another increase of the temperature (i.e. it is now equal to 15) and
also another iteration, i.e. a new activation of both [*] and [CheckTemp]. Now, since 15 = 15, [CheckTemp]
sets the heater’ state to ``off``. The predicate [=] is activated and it
returns ``false``. This time, the concept [+] is not activated by the guard
relation. The description of the concept [HeaterSystem
...] is no more active and so, its execution is finished. Since the type HeaterSystem is defined as a subtype of PROCEDURE_ACTIVITY,
the description of the concept [HeaterSystem] is
erased and its state becomes ``steady ; o``
(Figure 11.h).
![]()

5. Summary and future works
Conceptual Graphs theory has been proposed by John
Sowa as a graphic system of logic. The theory is composed of some basic
elements (CG structure, type hierarchy, conceptual structures, canon, context
and coreference) with canonical formation rules and
inference rules.
This paper described another use of the basic elements :
along with a context activation mechanism, the basic elements of the CG theory are used in a ``conceptual
formulation`` and integration of many programming paradigms (sequential and/or
parallel procedural, process, functional, event-driven and object oriented
paradigms). For computational purpose, a) the definition of coreference
is extended to include ``compound coreference``, b)
states and lifecycles are associated to concepts and c) a finite set of data
and control relations (in, out, guard, next) are defined with propagation rules
as their procedural semantic.
The result is a graphic multi-paradigm
programming language, called SYNERGY. Computation model of
SYNERGY is defined as a context activation mechanism which is based on concept’
lifecycle and relation’ propagation rules.
We are using and developing SYNERGY
and its graphical environment in many ways. Two points for development are
related to the topic of this paper :
n
Implementation of SYNERGY on a multi-process platform. This is important
for real-time and multi-media applications, or when a user wants to call in
parallel from his SYNERGY program, processes that are defined in other
languages.
n
The use of ``micro-canons`` instead of one canon. Currently, all defined
types are specified in the canon (the long term memory). In some applications,
``artificial`` types are defined only to enable a modular and concise
definition of other types. In these cases, it could be better to define a
``main`` canon with micro-canons that group the artificial types according to
their specific purposes.
References
1. Brauer W., W. Reisig
and G. Rozenberg (eds.), Petri Nets: Applications and Relationships to Other Models of
Concurrency, Springer-Verlag, 1986.
2. Davis A. L. and R. M.
Keller, Data Flow Program Graphs, in
Computer, Feb. 1982 and in Thakkar (ed), 1987.
3. Ellis G., Object-Oriented Conceptual Graphs, Proc. Third International Conference on Conceptual Structures, ICCS’95, Santa Cruz, CA, 1995.
4. Esch J., Contexts as white box concepts, Proc. First International Conference on Conceptual
Structures, ICCS’93,
5. Esch J., Contexts and Concepts, Abstraction Duals, Proc. Second International Conference on Conceptual Structures, ICCS’94, College Park, Maryland, 1994a.
6. Esch J., Contexts, Canons and Coreferent Types,
Proc. Second International Conference on Conceptual Structures, ICCS’94,
7. Gaudiot J-L., Dataflow machines, in V. M. Milutinovic (ed), High-level language computer architecture, Computer
Science Press, 1989.
8. Hee K. M., P. M. P. Rambags
and P. A. C. Verkoulen, Specification and Simulation with ExSpect,
in Lauer (Ed), Functional Programming, Concurrency, Simulation and Automated
Reasoning, Springer-Verlag, 1993.
9. Hines T. R., J. C. Oh
and M. A. Hines, Object-Oriented
Conceptual Graphs, in Proc. of the Fifth Annual Workshop on Conceptual
Structures, 1990.
10. Janson S. and Haridi
S., An Introduction to AKL, A Multi-Paradigm
Programming Language, (via WWW), 1993.
11. Kabbaj A. and C. Frasson, Dynamic CG: Toward a General Model of Computation, Proc. Third International Conference on Conceptual Structures, ICCS’95, Santa Cruz, CA, 1995.
12. Kabbaj A., Rouane
K. and Frasson C., The use of a semantic network activation language in an ITS project,
Third International Conference on Intelligent Tutoring Systems, ITS’96,
Springer-Verlag, 1996.
13. Kabbaj A., Un système multi-paradigme pour la manipulation des connaissances utilisant la théorie des graphes conceptuels, Ph.D Thesis, DIRO, U. de Montréal, June, 1996.
14. Kabbaj A., SYNERGY as a concurrent object oriented language, submitted to
Fifth International Conference on Conceptual Structures, ICCS’97.
15. Lakos C., From Coloured Petri Nets to Object Petri Nets, in Michelis G. and M. Diaz (Eds.), Application and Theory of
Petri Nets, Springer, 1995.
16. Liddle S. W., D. W. Embley
and S. N. Woodfield, A Seamless Model for Object-Oriented System development, Bertino E. and S. Urban (Eds.), Object-Oriented
Methodologies and Systems, Springer-Verlag, 1994.
17. Lukose D., Executable conceptual structures, Proc. First International Conference on Conceptual
Structures, ICCS’93,
18. Madsen O., B. Moller-Pedersen and K. Nygaard, Obejct-Oriented Programming in the BETA
Programming Language, Addison-Wesley, 1993.
19. Norman D. A., D. E. Rumelhart and the LNR group, Explorations in Cognition, W. H. Freeman and Company, 1975.
20. Sargeant J., Uniting Functional and Object-Oriented Programming, in Nishio S. and A. Yonezawa (Eds.),
Object Tehnologies for Advanced Software, Springer-Verlag,
1993.
21. Shlaer S. and S. J. Mellor, Object Lifecycles - Modeling
the World in States, Prentice-Hall, 1992.
22. Smolka G., An Oz Primer, (via WWW), 1995.
23. Sowa J. F., Conceptual Structures :
Information Processing in Mind and Machine, Addison-Wesley, 1984.
24. Sowa J. F., Conceptual Graphs as a universal knowledge
representation, in Lehmann (ed), Special Issue on
Semantic networks in artificial intelligence, in an International Journal computers & mathematics with
applications, 23:2-9, 1992.
25. Sowa J. F., Relating Diagrams to Logic, Proc. First
International Conference on Conceptual Structures, ICCS’93,
26. Sowa J. F., Logical foundations for representing
object-oriented systems, J. of Experimental and Theoretical AI, 5, 1993b.
27. Thakkar S. S. (ed.), Selected Reprints on Dataflow and Reduction Architectures, IEEE
Computer Society Press, 1987.
28. Törn A. A., Systems Modelling and Analysis Using Simulation Nets, in C. A. Kulikowski and al. (eds.), Artificial Intelligence and
Expert Systems Languages in Modelling and Simulation, Elsevier Science North-Holland, 1988.
29. Wuwongse V. and B. G. Ghosh, Towards Deductive Objective-Oriented
Databases Based on Conceptual Graphs, in Proc. of the 7th Annual Workshop
on Conceptual Structures, 1992.